===
Index
模板
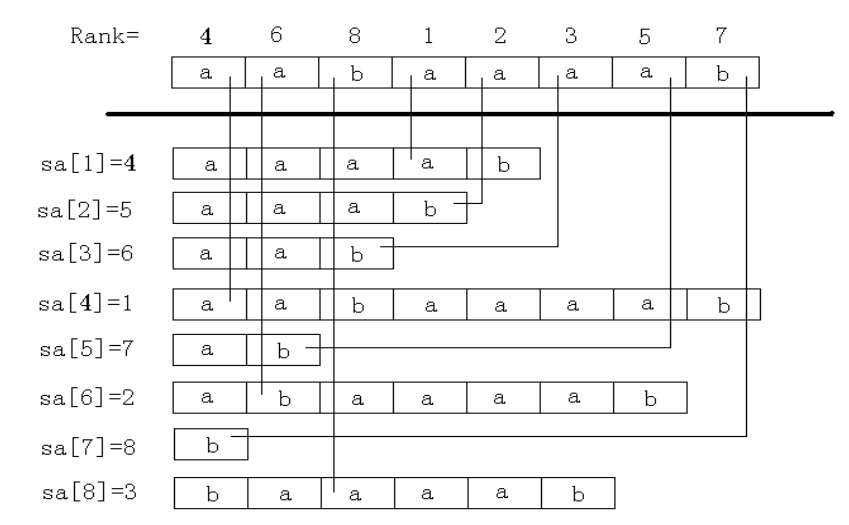
后缀数组主要关系两个数组: sa和rk,
sa[i]表示表示将所有后缀排序后第i小的后缀的编号.
rk[i]表示后缀i的排名,这两个数组满足性质:
sa[rk[i]] = rk[sa[i]] = i
template<typename T>
struct ST {
int n = 0;
vector<vector<T>> mat;
static int largest_bit(int x) { return 31 - __builtin_clz(x);}
ST(const vector<T> &a = {}) { if (!a.empty()) build(a);}
void build(const vector<T> &a) {
n = int(a.size());
int max_log = largest_bit(n) + 1;
mat.resize(max_log);
for (int k = 0; k < max_log; k++)
mat[k].resize(n - (1 << k) + 1);
if (n > 0) mat[0] = a;
for (int k = 1; k < max_log; k++)
for (int i = 0; i <= n - (1 << k); i++)
mat[k][i] = min(mat[k - 1][i], mat[k - 1][i + (1 << (k - 1))]);
}
T get_val(int a, int b) const {
assert(0 <= a && a < b && b <= n);
int t = largest_bit(b - a);
return min(mat[t][a], mat[t][b - (1 << t)]);
}
};
template <class T = int, bool build_lcp = false>
struct SA {
int n = -1;
vector<int> sa, rnk, lcp, s2;
ST<int> st;
SA(): n(0) {}
SA(const vector<T>& s) : n(s.size()), s2(n) {
vector<int> idx(n);
iota(idx.begin(), idx.end(), 0);
sort(idx.begin(), idx.end(), [&](int l, int r) { return s[l] < s[r]; });
int now = 0;
for (int i = 0; i < n; ++i) {
if (i && s[idx[i - 1]] != s[idx[i]]) now++;
s2[idx[i]] = now;
}
get_suffix_array(s2, now);
if (build_lcp) lcp_array(s2);
}
SA(const string& s) : n(s.size()), s2(n){
for (int i = 0; i < n; ++i) s2[i] = s[i];
get_suffix_array(s2, 255);
if (build_lcp) lcp_array(s2);
}
void get_suffix_array(vector<int>& s, int upper) {
assert(0 <= upper);
for (int d : s) assert(0 <= d && d <= upper);
sa = sa_is(s, upper);
}
vector<int> sa_naive(const vector<int>& s) {
int n = int(s.size());
vector<int> sa(n);
iota(sa.begin(), sa.end(), 0);
sort(sa.begin(), sa.end(), [&](int l, int r) {
if (l == r) return false;
while (l < n && r < n) {
if (s[l] != s[r]) return s[l] < s[r];
l++, r++;
}
return l == n;
});
return sa;
}
vector<int> sa_doubling(const vector<int>& s) {
int n = int(s.size());
vector<int> sa(n), rnk = s, tmp(n);
iota(sa.begin(), sa.end(), 0);
for (int k = 1; k < n; k *= 2) {
auto cmp = [&](int x, int y) {
if (rnk[x] != rnk[y]) return rnk[x] < rnk[y];
int rx = x + k < n ? rnk[x + k] : -1, ry = y + k < n ? rnk[y + k] : -1;
return rx < ry;
};
sort(sa.begin(), sa.end(), cmp);
tmp[sa[0]] = 0;
for (int i = 1; i < n; i++)
tmp[sa[i]] = tmp[sa[i - 1]] + (cmp(sa[i - 1], sa[i]) ? 1 : 0);
swap(tmp, rnk);
}
return sa;
}
template <int THRESHOLD_NAIVE = 10, int THRESHOLD_DOUBLING = 40>
vector<int> sa_is(const vector<int>& s, int upper) {
int n = int(s.size());
if (n == 0) return {}; if (n == 1) return {0};
if (n == 2) { if (s[0] < s[1]) return {0, 1}; else return {1, 0};}
if (n < THRESHOLD_NAIVE) return sa_naive(s);
if (n < THRESHOLD_DOUBLING) return sa_doubling(s);
vector<int> sa(n), sum_l(upper + 1), sum_s(upper + 1);
vector<bool> ls(n);
for (int i = n - 2; i >= 0; i--)
ls[i] = (s[i] == s[i + 1]) ? ls[i + 1] : (s[i] < s[i + 1]);
for (int i = 0; i < n; i++) {
if (!ls[i]) sum_s[s[i]]++;
else sum_l[s[i] + 1]++;
}
for (int i = 0; i <= upper; i++) {
sum_s[i] += sum_l[i];
if (i < upper) sum_l[i + 1] += sum_s[i];
}
auto induce = [&](const vector<int>& lms) {
fill(sa.begin(), sa.end(), -1);
vector<int> buf(upper + 1);
copy(sum_s.begin(), sum_s.end(), buf.begin());
for (auto d : lms) {
if (d == n) continue;
sa[buf[s[d]]++] = d;
}
copy(sum_l.begin(), sum_l.end(), buf.begin());
sa[buf[s[n - 1]]++] = n - 1;
for (int i = 0; i < n; i++) {
int v = sa[i];
if (v >= 1 && !ls[v - 1]) sa[buf[s[v - 1]]++] = v - 1;
}
copy(sum_l.begin(), sum_l.end(), buf.begin());
for (int i = n - 1; i >= 0; i--) {
int v = sa[i];
if (v >= 1 && ls[v - 1]) sa[--buf[s[v - 1] + 1]] = v - 1;
}
};
vector<int> lms_map(n + 1, -1), lms;
int m = 0;
for (int i = 1; i < n; i++) {
if (!ls[i - 1] && ls[i]) lms_map[i] = m++;
}
lms.reserve(m);
for (int i = 1; i < n; i++) if (!ls[i - 1] && ls[i]) lms.push_back(i);
induce(lms);
if (m) {
vector<int> sorted_lms, rec_s(m);
sorted_lms.reserve(m);
for (int v : sa)
if (lms_map[v] != -1) sorted_lms.push_back(v);
int rec_upper = 0;
rec_s[lms_map[sorted_lms[0]]] = 0;
for (int i = 1; i < m; i++) {
int l = sorted_lms[i - 1], r = sorted_lms[i];
int end_l = (lms_map[l] + 1 < m) ? lms[lms_map[l] + 1] : n;
int end_r = (lms_map[r] + 1 < m) ? lms[lms_map[r] + 1] : n;
bool same = true;
if (end_l - l != end_r - r) same = false;
else {
while (l < end_l) {
if (s[l] != s[r]) break;
l++, r++;
}
if (l == n || s[l] != s[r]) same = false;
}
if (!same) rec_upper++;
rec_s[lms_map[sorted_lms[i]]] = rec_upper;
}
auto rec_sa = sa_is<THRESHOLD_NAIVE, THRESHOLD_DOUBLING>(rec_s, rec_upper);
for (int i = 0; i < m; i++)
sorted_lms[i] = lms[rec_sa[i]];
induce(sorted_lms);
}
return sa;
}
void get_rnk() {rnk.resize(n); for(int i = 0; i < n; ++i) rnk[sa[i]] = i;}
void lcp_array(vector<T>& s) {
assert(n >= 1);
get_rnk();
lcp.assign(n - 1, 0);
int h = 0;
for (int i = 0; i < n; ++i) {
if (h > 0) h--;
if (rnk[i] == 0) continue;
int j = sa[rnk[i] - 1];
for (; j + h < n && i + h < n; h++)
if (s[j + h] != s[i + h]) break;
lcp[rnk[i] - 1] = h;
}
}
bool contains(const string& s) { // 是否包含子串s O(mlog(n))
int m = s.size();
auto cmp = [&](int x) {
for (int j = 0; x + j < n and j < m; ++j) {
if (s2[x + j] < s[j]) return -1;
if (s2[x + j] > s[j]) return 1;
}
return n - x < m ? -1 : 0;
};
int l = 0, r = n - 1;
while (l <= r) {
int md = (l + r) / 2;
int c = cmp(sa[md]);
if (c == 0) return true;
else if (c < 0) l = md + 1;
else r = md - 1;
}
return false;
}
int count(const string& s) { // s作为子串的出现次数 O(mlog(n))
int m = s.size();
if (n < m) return 0;
auto lower = [&](int h) {
for (int j = 0; h + j < n and j < m; j++) {
if (s2[h + j] < s[j]) return true;
if (s2[h + j] > s[j]) return false;
}
return n - h < m;
};
auto upper = [&](int h) {
for (int j = 0; h + j < n and j < m; j++)
if (s2[h + j] > s[j]) return false;
return true;
};
const auto L = partition_point(sa.begin(), sa.end(), lower);
const auto R = partition_point(L, sa.end(), upper);
return distance(L, R);
// return vector<int>(L, R); // 如果需要返回出现的位置
}
long long distinct_substr() const { // 不同子串的数目, assert(build_lcp = True)
long long res = n * (n + 1ll) / 2;
for (int x : lcp)
res -= x;
return res;
}
//返回s,t的最长公共子串<s中的下标,长度>,传入 s+'#'+t,m为s.size()
pair<int, int> longest_common_substr(int m) { // assert(build_lcp = True)
int len = 0, idx = 0;
for (int i = 0; i < n - 1; ++i) {
if ((sa[i] < m) != (sa[i + 1] < m) && lcp[i] > len)
len = lcp[i], idx = sa[i];
}
return {idx, len};
}
void build_rmq() {vector<int> a(n);for(int i=1; i<n; ++i) a[i]=lcp[i-1]; st.build(a);}
int get_lcp_from_ranks(int a, int b) const { //保证build_rmq已执行
if (a == b) return n - sa[a];
if (a > b) swap(a, b);
return st.get_val(a + 1, b + 1);
}
int get_lcp(int a, int b) const { //s[a:n-1],s[b:n-1]的最长公共前缀
if (a >= n || b >= n) return 0;
if (a == b) return n - a;
return get_lcp_from_ranks(rnk[a], rnk[b]);
}
int comp(int a, int b, int len = -1) const { //O(1)时间比较s[a:a+len-1],s[b:b+len-1]
if (len < 0) len = n; if (a == b) return 0;
int k = get_lcp(a, b); if (k >= len) return 0;
if (a + k >= n || b + k >= n) return a + k >= n ? -1 : 1;
return s2[a + k] < s2[b + k] ? -1 : (s2[a + k] == s2[b + k] ? 0 : 1);
}
void sort_substrs(vector<array<int, 2>> &qs) { // a[i]: s[l..r-1]
sort(qs.begin(), qs.end(), [&](array<int, 2> &a, array<int, 2> &b){
int n1 = a[1] - a[0], n2 = b[1] - b[0], cmp = comp(a[0], b[0], min(n1, n2));
if (cmp != 0) return cmp < 0;
return n1 != n2 ? n1 < n2 : (a < b);
});
}
long long count_borders() const { // assert(build_lcp = True)
long long ans = (n + 1ll) * n / 2, s = 0;
vector<pair<int,int>> sk;
for (int i = 1; i < n; ++i) {
int len = lcp[i - 1], cnt = 1;
while (!sk.empty() && len <= sk.back().first) {
s -= sk.back().first * 1ll * sk.back().second;
cnt += sk.back().second;
sk.pop_back();
}
sk.emplace_back(len, cnt);
s += len * 1ll * cnt;
ans += s;
}
return ans;
}
};
使用方法
- 构造字符串的后缀数组
SA<int> sa(s); //sa.sa 即为后缀数组,长度n,下标从0开始。
- 获取字符串的lcp数组
需将build_lcp置为1,lcp长度n-1, lcp[i]=lcp(sa[i],sa[i+1])
string s = "abcac";
SA<int, 1> sa(s);
auto lcp = sa.lcp;
判断子串
给定长为n字符串s,q次询问,每次询问给定字符串t,判断t是否为s的子串。
- 1 <= n, q<= 3e5
- t字符串总长度不超过3e5
// SA 模板
void ac_yyf(int tt) {
string s, t;
int q;
cin >> s >> q;
SA<int> sa(s);
for (int i = 0; i < q; ++i) {
cin >> t;
cout << (sa.contains(t) ? "Yes" : "No") << '\n';
}
}
统计子串
给定长为n字符串s,q次询问,每次询问给定字符串t,统计s有多少个子串等于t。
- 1 <= n, q<= 3e5
- t字符串总长度不超过3e5
// SA
void ac_yyf(int tt) {
string s, t;
int q;
cin >> s >> q;
SA<int> sa(s);
for (int i = 0; i < q; ++i) {
cin >> t;
cout << sa.count(t) << '\n';
}
}
不同子串数目
给定一个字符串,求字符串的不同的非空子串数目
- 1 <= n <= 5e5
- s 仅包含小写字母
// SA
void ac_yyf(int tt) {
string s;
cin >> s;
SA<int, 1> sa(s);
cout << sa.distinct_substr() << '\n';
}
s和t的最长公共子串
求s和t的最长公共子串,如果有多个答案,输出字典序最小的。
- 1 <= n, m <= 1e5
void ac_yyf(int tt) {
string s, t;
cin >> s >> t;
int n = s.size();
s += '#';
s += t;
SA<int, 1> sa(s);
auto [idx, len] = sa.longest_common_substr(n);
cout << s.substr(idx, len) << '\n';
}
子串排序
给定字符串s,和一个子串数组qs,qs[i]表示为[l,r],表示子串s[l..r], 根据字典序对qs进行排序。
- 1 <= n, m <= 4e5
- 1 <= l <= r <= n
void ac_yyf() {
cin >> s >> q;
vector<array<int, 2>> qs(q);
for (int i = 0; i < q; ++i) {
cin >> qs[i][0] >> qs[i][1];
qs[i][0]--;
}
SA<int, 1> sa(s);
sa.build_rmq(); // 注意调用build_rmq
sa.sort_substrs(qs);
for(auto& [x,y]:qs){
cout << x + 1 << ' ' << y << '\n';
}
}
所有子串borders总和
如果字符串t既是字符串s的前缀也是s的后缀,则称t是s的border,空串是s的border,但s本身不算。给定字符串s,求s的所有子串的borders数目总和。
- 1 <= n <= 4e5
void ac_yyf() {
string s;
cin >> s;
SA<int, 1> sa(s);
cout << sa.count_borders() << '\n';
}
最大循环子串
给定字符串s,求最大的整数k,满足存在一个非空字符串拼接k次后形成的字符串是s的子串。
- 1 <= n <= 4e5
// SA
int periodic_substr(string &s) {
int n = s.size(), ans = 1;
SA<int, 1> s1(s);
s1.build_rmq();
reverse(s.begin(), s.end());
SA<int, 1> s2(s);
s2.build_rmq();
for (int len = 1; len <= n; ++len) {
for (int l = 0, r = len - 1; l < n; l = r + 1) {
while (r + len < n && s1.get_lcp(l, r + 1) >= len) r += len;
if (l > r) break;
int cl = l, cr = r;
if (r + 1 < n) cr += s1.get_lcp(l, r + 1);
if (l - 1 >= 0) cl -= s2.get_lcp(n - 1 - (l - 1), n - 1 - r);
ans = max(ans, (cr - cl + 1) / len);
}
}
return ans;
}
void ac_yyf() {
string s;
cin >> s;
cout << periodic_substr(s) << '\n';
}
从字符串首尾取字符最小化字典序
给你一个字符串,每次从首或尾取一个字符组成字符串,问所有能够组成的字符串中字典序最小的一个。
- 1 <= n <= 1e6
将字符串s和s的逆序拼接成新的字符串,计算rnk数组,每次取rnk较小的字符
// SA
string minLogicStr(string &s) {
string t = s, ans;
reverse(t.begin(), t.end());
s = s + t;
int n = s.size(), l = 0, r = t.size() - 1;
SA<int, 1> sa(s);
auto rk = sa.rnk;
while (l <= r) {
if (rk[l] < rk[n - 1 - r]) ans += s[l++];
else ans += s[r--];
}
return ans;
}
m个数组的最长公共子数组
输入n和m个数组,每个元素在[0,n-1)之间,求m个数组的最长公共子数组长度。
- 1 <= n <= 1e5
- 2 <= m <= 1e5
- sum(mi) <= 1e5
// SA
int longest_common_subarr(int n, vector<vector<int>> &qs) {
int tot = 0, m = qs.size(), l = 0, r = 1e9, sum = 0, ans = 0;
for (auto &v : qs) { sum += v.size();}
vector<int> pos(sum + m - 1), a(sum + m - 1);
for (int i = 0; i < m; ++i) {
int t = qs[i].size();
if (t < r) r = t;
for (int j = 0; j < t; ++j) {
pos[tot] = i;
a[tot++] = qs[i][j];
}
if (i + 1 < m) a[tot++] = n + i;
}
SA<int, 1> sa(a);
while (l <= r) {
int md = (l + r) / 2, ok = 0;
vector<int> vis(m);
for (int i = 1; i < tot; ++i) {
if (sa.lcp[i - 1] >= md) {
int j = i, cnt = 0;
for (; j < tot && sa.lcp[j - 1] >= md; j++);
for (int k = i - 1; k < j; ++k) if (!vis[pos[sa.sa[k]]]++)
cnt++;
for (int k = i - 1; k < j; ++k)
vis[pos[sa.sa[k]]]--;
i = j - 1;
if (cnt >= m) {ok = 1; break;}
}
}
if (ok) {ans = md; l = md + 1;}
else r = md - 1;
}
return ans;
}





