快速沃尔什变换

2023-01-20 | 阅读：次

===

Index

简介与模板
异或例题
按位与例题
- 所有子数组按位与和之和
- 按位与奇数个1异或偶数个1的子数组数目
按位或例题

简介与模板

沃尔什转换（Walsh Transform）是在频谱分析上作为离散傅立叶变换的替代方案的一种方法。

其实这个变换在信号处理中应用很广泛，fft是double类型的，但是walsh把信号在不同震荡频率方波下拆解，因此所有的系数都是绝对值大小相同的整数，这使得不需要作浮点数的乘法运算，提高了运算速度。

所以，FWT和FFT的核心思想应该是相同的。都是对数组的变换。我们设数组A经过快速沃尔什变换之后记作

FWT[A]

那么FWT核心思想就是：

我们需要一个新序列C，由序列A和序列B经过某运算规则得到，即

C = A # B

。我们先正向得到 FWT[A], FWT[B]

然后根据 FWT[C] = FWT[A] * FWT[B] * 为点乘, 在O(n)求出 FWT[C], ,然后再逆向运算得到原序列C。时间复杂度为 O(nlog(n))

在算法竞赛中，FWT是用于解决对下标进行位运算卷积问题的方法。

C[i] = sum(A[j] * B[k]) for all (j # k = i) 其中 # 是任意二元位运算中的某一种，* 是普通乘法。

或运算

模板

template <bool _Forward, typename _Iterator>
void FWT_bitor(_Iterator first, _Iterator last) {
    const uint32_t length = last - first;
    for (uint32_t i = 1; i < length; i <<= 1)
        for (uint32_t j = 0; j < length; j += i << 1)
            for (auto it = first + j, it2 = first + j + i, end = first + j + i; it != end; ++it, ++it2) {
                auto x = *it, y = *it2;
                if constexpr (_Forward)
                    *it2 = x + y;
                else
                    *it2 = y - x;
            }
}

使用方法

参数：_Forward 为 true，表示前向求 FWT 过程， false 表示反演求 UWFT过程
参数：_Iterator 迭代器类型

示例：

vector<int> a(n);
FWT_bitxor<true, vector<int>::iterator>(a.begin(), a.end());

与运算

与运算类比或运算可以得到类似结论

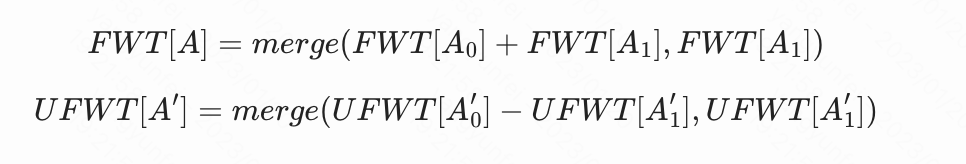
模板

template <bool _Forward, typename _Iterator>
void FWT_bitand(_Iterator first, _Iterator last) {
    const uint32_t length = last - first;
    for (uint32_t i = 1; i < length; i <<= 1)
        for (uint32_t j = 0; j < length; j += i << 1)
            for (auto it = first + j, it2 = first + j + i, end = first + j + i; it != end; ++it, ++it2) {
                auto x = *it, y = *it2;
                if constexpr (_Forward)
                    *it = x + y;
                else
                    *it = x - y;
            }
}

异或运算

模板

template <bool _Forward, typename _Iterator>
void FWT_bitxor(_Iterator first, _Iterator last) {
    const uint32_t length = last - first;
    for (uint32_t i = 1; i < length; i <<= 1)
        for (uint32_t j = 0; j < length; j += i << 1)
            for (auto it = first + j, it2 = first + j + i, end = first + j + i; it != end; ++it, ++it2) {
                auto x = *it, y = *it2;
                if constexpr (_Forward)
                    *it = x + y, *it2 = x - y;
                else
                    *it = (x + y) / 2, *it2 = (x - y) / 2;
            }
}

同或运算

异或例题

统计异或值在范围内的数对有多少

leetcode 1803

长为n的数组a,及两个整数 low 和 high, 求满足 low <= a[i] ^ a[j] <= high, 0 <= i < j < n 的 (i,j) 对的数目。

1 <= n <= 2e4
1 <= a[i] <= 2e4
1 <= low <= high <= 2e4

沃尔什变换解法

template <bool _Forward, typename _Iterator>
void FWT_bitxor(_Iterator first, _Iterator last) {
    const uint32_t length = last - first;
    for (uint32_t i = 1; i < length; i <<= 1)
        for (uint32_t j = 0; j < length; j += i << 1)
            for (auto it = first + j, it2 = first + j + i, end = first + j + i; it != end; ++it, ++it2) {
                auto x = *it, y = *it2;
                if constexpr (_Forward)
                    *it = x + y, *it2 = x - y;
                else
                    *it = (x + y) / 2, *it2 = (x - y) / 2;
            }
}

class Solution {
public:
    int countPairs(vector<int>& a, int low, int high) {
        int N = 1 << 15, ans = 0;
        vector<int> cnt(N);
        for (auto x : a) 
            cnt[x]++;
        FWT_bitxor<true, vector<int>::iterator>(cnt.begin(), cnt.end());
        for (auto &x: cnt)
            x *= x;
        FWT_bitxor<false, vector<int>::iterator>(cnt.begin(), cnt.end());
        for (int i = low; i <= high; ++i) 
            ans += cnt[i];
        return ans / 2;
    }
};

频率最高的子序列异或和

hackerRank xor subsequences

一个长度为n的数组a有 n * (n+1)/2 个非空子数组，每个子数组有一个异或和，求所有子数组异或和中出现次数最多的那个数的数值，以及该数值的出现次数。

1 <= n <= 1e5
1 < a[i] <= 2e16

沃尔什变换解法

设 s 为 a 的前缀异或和，对于a中的一个子数组a[i,j] 其异或和对应于 s中的一个pair对 (i-1,j), 问题可转化为上面的问题。

由于 cnt 对于 i=0,..n-1都会计算 s[i,i]的异或和，相当于多计算了n次a中的空数组，所以最后 cnt[0] -= n。考虑对s统计的(0,i)对的意义，对应原数组a 为a[1,..i]的异或和，所以每个 a[0..i]的异或和都少计算了一次。

vector<int> xorSubsequence(vector<int> a) {
    int n = a.size(), N = 1 << 16;
    vector<long long> cnt(N);
    for (int i = 0; i < n; ++i) {
        if (i > 0) a[i] ^= a[i - 1];
        cnt[a[i]]++;
    }
    FWT_bitxor<true, vector<long long>::iterator>(cnt.begin(), cnt.end());
    for (int i = 0; i < N; ++i) 
        cnt[i] *= cnt[i];
    FWT_bitxor<false, vector<long long>::iterator>(cnt.begin(), cnt.end());
    cnt[0] -= n;   
    for (auto &x : cnt) 
        x /= 2;
    for (int i = 0; i < n; ++i) 
        ++cnt[a[i]];  

    int ans = 0;
    long long max_freq = 0;
    for (int i = 0; i < N; ++i) {
        if (cnt[i] > max_freq) {
            max_freq = cnt[i];
            ans = i;
        }
    }
    return {ans, max_freq};
}

所有子数组异或和之和

一个长度为n的数组a有 n * (n+1)/2 个非空子数组，每个子数组有一个异或和，求所有子数组异或和的总和。

1 <= n <= 1e5
1 < a[i] <= 2^31

分析

本题可使用上一题的cnt 数组计算(在a[i]元素不太大时)，同时也可以按位计算对结果的贡献，先前缀异或，从左向右扫记录二进制前缀的1，0个数，xor[i]==xor[j]^1的时候就加上这一位的权值，时间复杂度 O(nlog(n))

long long subXorsum(vector<int> &a) {
    int n = a.size(), mx = (*max_element(a.begin(), a.end()));
    int m = max(32 - (int)__builtin_clz(mx), 1);
    vector<int> s(n + 1);
    for (int i = 0; i < n; ++i) {
        s[i + 1] = s[i] ^ a[i];
    }
    vector<array<int, 2>> f(m);
    long long ans = 0;

    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j < m; ++j) {
            int x = (s[i] >> j) & 1;
            ans += f[j][x ^ 1] * (1ll << j);
            f[j][x]++;
        }
    }
    return ans;
}

按位与例题

子数组与运算通用模版

考虑以i为终点的所有子数组，不同的按位与值最多有log(x)种，模板：

其中对于每个i，p数组从大到小保存从i开始按位与的所有可能取值，与取得该值的最小左端点下标。

template<typename F> 
void bitwise_and(vector<int> &a, F &&f) {
    vector<pair<int,int>> p, q;
    for (int n = a.size(), i = 0; i < n; ++i) {
        q.emplace_back(a[i], i);
        int k = 0;
        for (int j = 0; j < p.size(); ++j) {
            p[j].first &= a[i];
            if (p[j].first == q[k].first) {
                q[k].second = p[j].second;
            } else {
                q.emplace_back(p[j].first, p[j].second);
                k++;
            }
        }
        p = q;
        q.clear();
        for (int j = k; j >= 0; --j) {
            // 以[l, r-1]为左端点，i为右端点的所有子数组，按位与的值都为p[j].first
            int l = p[j].second, r = (j > 0 ? p[j - 1].second : i + 1);
            f(i, l, r, p[j].first);
        }
    } 
}

所有子数组按位与和之和

一个长度为n的数组a有 n * (n+1)/2 个非空子数组，每个子数组有一个按位与和，求所有子数组按位与和的总和。

1 <= n <= 1e5
1 < a[i] <= 1e9

long long bitandsum(vector<int> &a){
    int n=a.size();
    long long c=0;
    const int K=30;
    for(int i=0;i<K;++i){
        int p=0;
        for(int j=0;j<n;++j){
            if((a[j]>>i)&1){
                p++;
            }else {
                if(p) c+=(1<<i)*1ll*p*(p+1)/2;
                p=0;
            }
        }
        if(p) c+=(1<<i)*1ll*p*(p+1)/2;
    }
    return c;
}

按位与奇数个1异或偶数个1的子数组数目

hackerearth

给定长度为n的数组a，计算有多少个子数组满足，子数组的按位与和二进制表示中包含奇数个1，按位异或和包含偶数个1.

1 <= n <= 1e6
1 <= a[i] <= 1e9

分析

对于两个数x和y，如果x和y的二进制表示中包含1的个数的奇偶性相同，则异或和包含偶数个1，否则包含奇数个1. 则可以用前缀和维护任意子数组包含1的个数的奇偶性。

void solve() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];    
    }

    vector<int> s(n + 1), c(n + 1);
    for (int i = 0; i < n; ++i) {
        s[i + 1] = s[i] ^ a[i]; 
    }

    for (int i = 0; i <= n; ++i) {
        if (__builtin_popcount(s[i]) & 1) c[i] ++;
    }
    for (int i = 1; i <= n; ++i) {
        c[i] += c[i - 1];
    }
    
    long long ans = 0;

    bitwise_and(a, [&](int i, int l, int r, int val){
        if (__builtin_popcount(val) & 1) {
            int d = (__builtin_popcount(s[i + 1]) & 1);
            if (d == 1) {
                ans += c[r - 1] - (l > 0 ? c[l - 1] : 0);
            } else {
                ans += r - l - c[r - 1] + (l > 0 ? c[l - 1] : 0);
            }
        }
    });

    cout << ans << '\n';
}

按位或例题

子数组或运算通用模板

考虑以i为起点的所有子数组，不同的按位或值最多有log(x)种，模板：

其中对于每个i，p数组从大到小保存从i开始按位或的所有可能取值，与取得该值的最小左端点下标。例如: 设x=a[i]|a[i+1]|...|a[n-1], 则p[0].first = x, p[0].second表示取得x的最小左端点。 注意顺序p[0]是最大值，p.back()是等于a[i]的最小值。

template<typename F> 
void bitwise_or(vector<int> &a, F &&f) {
    vector<pair<int,int>> p;
    for (int n = a.size(), i = n - 1; i >= 0; --i) {
        p.emplace_back(0, i);
        p[0].first |= a[i];
        int k = 0;
        for (int j = 1; j < p.size(); ++j) {
            p[j].first |= a[i];
            if (p[k].first == p[j].first) 
                p[k].second = p[j].second;
            else p[++k] = p[j];
        }
        p.resize(k + 1);
        for (int j = k; j >= 0; --j) {
            // 以i为左端点，[l,r-1]中任意元素为右端点的子数组按位或的值都为p[j].first
            int l = p[j].second, r = (j > 0 ? p[j - 1].second : n);
            f(i, l, r, p[j].first);
        }
    }
}

所有子数组按位或和之和

一个长度为n的数组a有 n * (n+1)/2 个非空子数组，每个子数组有一个按位或和，求所有子数组按位或和的总和。

1 <= n <= 1e5
1 < a[i] <= 1e9

long long subarrOrSum(vector<int> &a) {
    const int K = 30;
    int n = a.size();
    long long s=0;
    for(int i=0;i<K;++i){
        long long cu=0,p=0;
        for(int j=0;j<n;++j){
            if((a[j]>>i)&1) {
                p=0;
            } else{
                p++;
                cu+=p;
            }
        }
        s+=(1ll<<i)*(n*(n+1ll)/2-cu);
    }
    return s;
}

按位或最大的最小子数组长度

leetcode 2411

给定长度为n的数组a，求长度为n的数组ans,ans[i]表示以i为起点，任意不小于i的j为终点的所有子数组的按位或的最大值，取得该最大值时的最小子数组长度。

1 <= n <= 1e5
1 <= a[i] <= 1e9

vector<int> smallestSubarrays(vector<int>& a) {
    int n = a.size();
    vector<int> ans(n);
    bitwise_or(a, [&](int i, int l, int r, int val){
        if(r == n) ans[i] = l - i + 1;
    });
    return ans;
}

按位或二进制包含奇数个1的子数组数量

hackerearth cir_8

给定长度为n的数组a，求有多少个子数组满足，该子数组按位或的二进制表示中包含奇数个1.

1 <= n <= 1e6
1 <= a[i] <= 1e9

void ac_yyf(int tt) {
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
    }
    long long ans = 0;
    bitwise_or(a, [&](int i, int l, int r, int val){
        if (__builtin_popcount(val) & 1) ans += r - l;
    });
    cout << ans << '\n';
}

按位或和出现在数组中的子数组数目

BNY Mellon OA

输入数组a,求非空子数组的数目，满足该子数组的按位或和与数组中的某个元素相等。

1 <= n <= 1e5 1 <= a[i] <= 1e6

分析

和上题基本相同，只需修改一下判断条件。

long long count_or_subarray(vector<int> &a) {
    int n = a.size();
    long long ans = 0;
    unordered_set<int> s(a.begin(), a.end());
    vector<pair<int,int>> p;
    for (int i = n - 1; i >= 0; --i) {
        p.emplace_back(0, i);
        p[0].first |= a[i];
        int k = 0;
        for (int j = 1; j < p.size(); ++j) {
            p[j].first |= a[i];
            if (p[k].first == p[j].first) 
                p[k].second = p[j].second;
            else p[++k] = p[j];
        }
        p.resize(k + 1);
        for (int j = k; j >= 0; --j) {
            if (s.count(p[j].first)) 
                ans += (j > 0 ? p[j - 1].second : n) - p[j].second;
        }
    } 
    return ans;
}

统计所有子数组按位或的出现次数

一个长度为n的数组a有 n * (n+1)/2 个非空子数组，每个子数组有一个按位或和，求所有子数组按位或和的出现次数。

1 <= n <= 1e5
1 <= a[i] <= 1e9

map<int, int> count_or_freq(vector<int> &a) {
    int n = a.size();
    map<int, int> mp;
    vector<pair<int,int>> p;
    for (int i = n - 1; i >= 0; --i) {
        p.emplace_back(0, i);
        p[0].first |= a[i];
        int k = 0;
        for (int j = 1; j < p.size(); ++j) {
            p[j].first |= a[i];
            if (p[k].first == p[j].first) 
                p[k].second = p[j].second;
            else p[++k] = p[j];
        }
        p.resize(k + 1);
        for (int j = k; j >= 0; --j) {
            mp[p[j].first] += (j > 0 ? p[j - 1].second : n) - p[j].second;
        }
    } 
    return mp;
}

king-yyf