莫队算法

2023-01-25 | 阅读：次

===

Index

普通莫队
树上莫队

简介与模版

莫队，是一种解决区间查询等问题的离线算法，基于分块思想，复杂度为 O(n·sqrt(n)) 。

一般来说，如果可以在 O(1) 内从 [l,r] 的答案转移到 [l-1,r], [l+1,r], [l,r-1], [l,r+1] 这四个与之紧邻的区间的答案，则可以考虑使用莫队。

模板

struct Mo {
  int width;
  vector<int> left, right, order;

  Mo(int N, int Q) : order(Q) {
    width = max<int>(1, 1.0 * N / max<double>(1.0, sqrt(Q * 2.0 / 3.0)));
    iota(begin(order), end(order), 0);
  }

  void insert(int l, int r) { /* [l, r) */
    left.emplace_back(l);
    right.emplace_back(r);
  }

  template <typename AL, typename AR, typename DL, typename DR, typename REM>
  void run(const AL &add_left, const AR &add_right, const DL &delete_left,
           const DR &delete_right, const REM &rem) {
    assert(left.size() == order.size());
    sort(begin(order), end(order), [&](int a, int b) {
      int ablock = left[a] / width, bblock = left[b] / width;
      if (ablock != bblock) return ablock < bblock;
      if (ablock & 1) return right[a] < right[b];
      return right[a] > right[b];
    });
    int nl = 0, nr = 0;
    for (auto idx : order) {
      while (nl > left[idx]) add_left(--nl);
      while (nr < right[idx]) add_right(nr++);
      while (nl < left[idx]) delete_left(nl++);
      while (nr > right[idx]) delete_right(--nr);
      rem(idx);
    }
  }
};

使用

使用时需定义如下函数:

Mo mo(n, q);   // n个元素，q次询问

for (int i = 0, l, r; i < q; ++i) {
    cin >> l >> r;
    mo.insert(l, r);  //query [l, r - 1]
} 

vector<long long> ans(q);
auto add_l = [&](int x) {

};
auto add_r = [&](int x) {

};
auto del_l = [&](int x) {

};
auto del_r = [&](int x) {

};

auto rem = [&](int x) { ans[x] = ...; };
mo.run(add_l,add_r,del_l,del_r,rem);

区间中有多少个不同的数

给出一个序列a,和q个查询 [l, r]，问[l, r]中有多少个不同的数。

1 <= n <= 3e4
1 <= q <= 2e5
1 <= l <= r <= n
1 < a[i] < 1e6

#include<bits/stdc++.h>
using namespace std;

// 模版

int main() {
    ios::sync_with_stdio(false); 
    cin.tie(nullptr);

    int n, q, mx = 0;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];    
        mx = max(mx, a[i]);
    }
    cin >> q;
    Mo mo(n, q);   // n个元素，q次询问
    for (int i = 0, l, r; i < q; ++i) {
        cin >> l >> r;
        mo.insert(l-1, r);  //query [l, r - 1]
    } 

    vector<int> ans(q), cnt(mx + 1);
    int cur = 0;
    auto add_l = [&](int x) {
        if (cnt[a[x]] == 0) cur++;
        cnt[a[x]]++;
    };
    auto add_r = [&](int x) {
        if (cnt[a[x]] == 0) cur++;
        cnt[a[x]]++;
    };
    auto del_l = [&](int x) {
        cnt[a[x]]--;
        if (cnt[a[x]] == 0) cur--;
    };
    auto del_r = [&](int x) {
        cnt[a[x]]--;
        if (cnt[a[x]] == 0) cur--;
    };

    auto rem = [&](int x) { ans[x] = cur; };
    mo.run(add_l,add_r,del_l,del_r,rem);

    for (int i = 0; i < q; ++i)
       cout << ans[i] << "\n";
}

区间中有多少个逆序对

给出一个序列a,和q个查询 [l, r)，问[l, r)中有多少个逆序对。

1 <= n, q <= 1e5
1 <= a[i] <= 1e9
0 <= l < r <= n

#include<bits/stdc++.h>
using namespace std;

// 模版

int main() {
    ios::sync_with_stdio(false);  cin.tie(nullptr);

    int n, q;
    cin >> n >> q;

    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];    
    }
    Mo mo(n, q);   // n个元素，q次询问
    for (int i = 0, l, r; i < q; ++i) {
        cin >> l >> r;
        mo.insert(l, r);  //query [l, r - 1]
    } 

    Discretization<int> v(a);   //离散化
    FenwickTree<int> b(v.size());
    for (int i = 0; i < n; ++i) {
        a[i] = v(a[i]); 
    }

    long long cnt = 0;
    vector<long long> ans(q);
    auto add_l = [&](int x) {
        cnt += b.ask(0, a[x] - 1);
        b.add(a[x], 1);
    };
    auto add_r = [&](int x) {
        cnt += b.ask(a[x] + 1, v.size());
        b.add(a[x], 1);
    };
    auto del_l = [&](int x) {
        cnt -= b.ask(0, a[x] - 1);
        b.add(a[x], -1);
    };
    auto del_r = [&](int x) {
        cnt -= b.ask(a[x] + 1, v.size());
        b.add(a[x], -1);
    };

    auto rem = [&](int x) { ans[x] = cnt; };
    mo.run(add_l,add_r,del_l,del_r,rem);

    for (int i = 0; i < q; ++i) 
        cout << ans[i] << " \n"[i == q - 1];
}

树上莫队

树上莫队是将树上的两个节点之间的路径转化为dfx序中的一个区间，再使用莫队算法，时间复杂度 O(q*sqrt(n)*log(n))

处理子树查询

可以通过先序dfs将树上节点顺序转化为数组的顺序，每个子树对应于数组中的一个区间，所以子树查询可以方便地转化为普通的莫队问题。

处理路径查询

当查询任意两点间路径的问题时，该路径上的节点可能并不对应于展平后数组的一个连续区间，例如两个人距离O(N)路径的节点在先序dfs中可能是相邻的。这里引入一种修改的dfs序，将一个节点分为进入该节点时间 ent[u] 和离开该节点时间 out[u], 如下图：

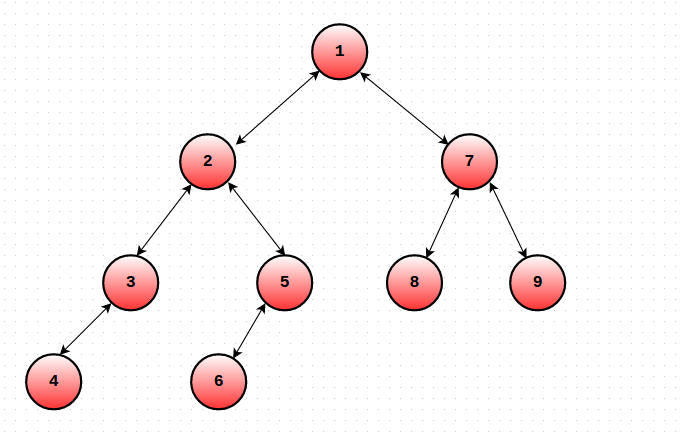
ent(1) = 1 out(1) = 18
ent(2) = 2 out(2) = 11
ent(3) = 3 out(3) = 6
ent(4) = 4 out(4) = 5
ent(5) = 7 out(5) = 10
ent(6) = 8 out(6) = 9
ent(7) = 12 out(7) = 17
ent(8) = 13 out(8) = 14
ent(9) = 15 out(9) = 16
dfs_ord = {1,2,3,4,4,3,5,6,6,5,2,7,8,8,9,9,7,1}

对于一个查询 (u, v), 不妨设 ent[u] < ent[v], 设 p = lca(u, v)，

如果 p = u, 则 (u,v)查询对应于dfs_ord的区间为 [ent[u], ent[v]]
p != v 查询对应的区间为 [out[u], ent[v]] + [ent[p], ent[p]]

模板

struct MoTree {
    int n, K, cur_ord;
    vector<vector<int>> g, fa;
    vector<int> dep, ent, out, dfs_ord;
    vector<array<int, 4>> qs;
 
    MoTree(int N, int Q) :n(N), cur_ord(-1){
        K = 32 - __builtin_clz(n);
        g.resize(n), fa.resize(n, vector<int>(K)), dep.resize(n);
        ent.resize(n), out.resize(n);
        dfs_ord.resize(n * 2);
    }
 
    void add_edge(int u, int v) {
        g[u].push_back(v);
        g[v].push_back(u);
    }
 
    void dfs(int id, int pa) {
        fa[id][0] = pa;
        ent[id] = ++cur_ord;
        dfs_ord[cur_ord] = id;
        for(auto& to: g[id]) if (to != pa){
            dep[to] = dep[id] + 1;
            dfs(to, id);
        }
        out[id] = ++cur_ord;
        dfs_ord[cur_ord] = id;
    }
 
    void build(int root = 0) {  // index of root
        dfs(root, -1);
        for(int j = 0; j < K-1; ++j) for(int i = 0; i < n; ++i) {
             if (fa[i][j] < 0) fa[i][j + 1] = -1;
             else fa[i][j + 1] = fa[fa[i][j]][j];
        }
    }
 
    int lca(int u, int v) {
        if (dep[u] > dep[v]) swap(u, v);
        for (int k = 0; k < K; k++) {
            if ((dep[v] - dep[u]) >> k & 1) {
                v = fa[v][k];
            }
        }
        if (u == v) return u;
        for (int k = K - 1; k >= 0; k--)
            if (fa[u][k] != fa[v][k]) {
                u = fa[u][k];
                v = fa[v][k];
            }
        return fa[u][0];
    }
 
    void insert(int l, int r, int u, int id) {  // [l, r, lca, id]
        qs.push_back({l, r, u, id});
    }
 
    template <typename REM, typename CHK>
    void run(const REM &rem, const CHK &chk) {
        
        int m = dfs_ord.size(), width = sqrt(m);
        vector<int> bl(m);
        for (int i = 0; i < bl.size(); i++) 
            bl[i] = i / width + 1;
        sort(begin(qs), end(qs), [&](auto &x, auto &y){
            if (bl[x[0]] != bl[y[0]]) return bl[x[0]] < bl[y[0]];
            return (bl[x[0]] & 1) ? x[1] < y[1] : x[1] > y[1];
        });
        int nl = qs[0][0], nr = nl - 1;

        for (auto &[l, r, p, id]: qs) {
            while (nl < l) chk(dfs_ord[nl++]);
            while (nl > l) chk(dfs_ord[--nl]);
            while (nr < r) chk(dfs_ord[++nr]);
            while (nr > r) chk(dfs_ord[nr--]);
            int u = dfs_ord[nl], v = dfs_ord[nr];
            if (p != u && p != v) chk(p);
            rem(id);
            if (p != u && p != v) chk(p);
        }
    }
};

树上统计2

spoj cot2

一颗n个节点的树，编号1-n，每个节点有一个权值。q个询问，每个询问给定(u,v)，求从u到v经过到节点路径上有多少个不同的数。

2 <= n <= 4e4
1 <= q <= 1e5
1 <= a[i] <= 1e9

#include<bits/stdc++.h>
using namespace std;

// MoTree, Discretization 模板
 
int main() {
    ios::sync_with_stdio(false); 
    cin.tie(nullptr);
 
    int n, q;
    cin >> n>> q;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];    
    }
    Discretization<int> v(a);
 
    for (int i = 0; i < n; ++i) {
        a[i] = v(a[i]);
    }
 
    MoTree mo(n, q);
 
    for(int i=0,u,v;i<n-1;++i){
        cin >> u >> v;
        u--, v--;
        mo.add_edge(u,v);
    }
    mo.build();
    for (int i = 0, l, r; i < q; ++i) {
        cin >> l >> r;
        l--, r--;
        int u = mo.lca(l, r);
        if (mo.ent[l] > mo.ent[r]) {
            swap(l, r);
        }
        if (u == l) {
            mo.insert(mo.ent[l], mo.ent[r], u, i);
        } else {
            mo.insert(mo.out[l], mo.ent[r], u, i);
        }
    }
    vector<int> ans(q), cnt(v.size()), vis(n);
    int cur = 0;
    auto check = [&](int x) {
        if (vis[x]) {
            if (--cnt[a[x]] == 0) cur--;
        } else {
            if (cnt[a[x]]++ == 0) cur++;
        }
        vis[x] ^= 1;
    };
    auto rem = [&](int x) { ans[x] = cur; };
    mo.run(rem, check);
    for (int i = 0; i < q; ++i) {
        cout << ans[i] << "\n";
    }
} 

路径查询

hackerearth path_query

给定一个n个节点的无向树，编号1-n，根节点是1，每个节点有一个值a[i],q个询问，每个询问给定 u,v，求u,v路径上的最大值+最小值+中位数之和。假设有路径上有k个节点，中位数定义为第(k+1)/2小的数。

1 <= n <= 4e4
1 <= q <= 1e5
1 <= a[i] <= 1e6

int main() {
    int n, q;
    cin >> n >> q;
    vector<int> a(n);
    int mx = 0;
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
    }

    MoTree mo(n,q);
    for (int i = 1, u,v; i < n; ++i) {
        cin>>u>>v;
        u--;
        v--;
        mo.add_edge(u,v);
    }

    mo.build();

    for(int i=0,l,r;i<q;++i){
        cin >> l >> r;
        l--, r--;
        int u = mo.lca(l, r);
        if (mo.ent[l] > mo.ent[r]) {
            swap(l, r);
        }
        if (u == l) {
            mo.insert(mo.ent[l], mo.ent[r], u, i);
        } else {
            mo.insert(mo.out[l], mo.ent[r], u, i);
        }
    }
    
    ordered_set<pair<int,int>> s;
    vector<int> vis(n),ans(q);
    auto check = [&](int x) {
        if (vis[x]) {
            s.erase({a[x],x});
        } else {
            s.insert({a[x],x});
        }
        vis[x] ^= 1;
    };
    auto rem = [&](int x) { 
        auto mx = *s.find_by_order(0);
        auto mn = *s.find_by_order(s.size() - 1);
        auto mid = *s.find_by_order((s.size() - 1) / 2);
        ans[x] = mx.first +mn.first+mid.first;
    };

    mo.run(rem, check);
    for (int i = 0; i < q; ++i) {
        cout << ans[i] << " \n"[i==q-1];
    }
}

树上逆序对

hackerearth_circuits_10

给定一个n个节点的树,每个节点有个值，节点i的值为a[i], q次询问，每次询问给定(u,v)，求从u到v经过节点的值形成的数组的逆序对数目加上从v到u经过节点的值形成的数组的逆序对数目。

2 <= n, q <= 1e5
1 <= a[i] <= n

分析

设节点u,v之间元素数目为N, 则从u到v和从v到u的逆序对总和等于 N(N-1)/2-sum(count[i]*(count[i]-1)/2)，可以使用莫队算法维护N和count的总和。

void ac_yyf(int tt) {
    int n, q;
    cin >> n >> q;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
        a[i]--;    
    }
    MoTree mo(n, q);
    for (int i = 0, u, v; i < n - 1; ++i) {
        cin >> u >> v;
        u--, v--;
        mo.add_edge(u, v);
    }
    mo.build();
    for (int i = 0, l, r; i < q; ++i) {
        cin >> l >> r;
        l--, r--;
        int u = mo.lca(l, r);
        if (mo.ent[l] > mo.ent[r]) {
            swap(l, r);
        }
        if (u == l) {
            mo.insert(mo.ent[l], mo.ent[r], u, i);
        } else {
            mo.insert(mo.out[l], mo.ent[r], u, i);
        }
    }
    vector<long long> ans(q);
    vector<int> cnt(n), vis(n);
    long long cur = 0, p = 0;
    auto check = [&](int x) {
        cur -= cnt[a[x]] * 1ll * (cnt[a[x]] - 1) / 2;
        if (vis[x]) {
            --cnt[a[x]];
            p--;
        } else {
            cnt[a[x]]++;
            p++;
        }
        cur += cnt[a[x]] * 1ll * (cnt[a[x]] - 1) / 2;
        vis[x] ^= 1;
    };
    auto rem = [&](int x) { ans[x] = p * 1ll * (p - 1) / 2 - cur; };
    mo.run(rem, check);
    for (int i = 0; i < q; ++i) {
        cout << ans[i] << "\n";
    }
}

king-yyf