===
Index
daimayuan
子串的最大差
定义序列的最大差为序列中最大数与最小数的差。比如 (3,1,4,5,6) 的最大差为 6−1=5 , (2,2) 的最大差为 2−2=0 。
定义一个序列的子串为该序列中连续的一段序列。
给定一个长度为 𝑛 的数组 𝑎1,𝑎2,…,𝑎𝑛,请求出这个序列的所有子串的最大差之和。
- 1 ≤ 𝑛 ≤ 500000
- 0 ≤ 𝑎𝑖 ≤ 1e8
分析
子序列的最大数和最小数相互独立,分别计算序列的所有子串的最大值和和最小值和,再求差。
long long calc(vector<int> &a){
int n = a.size();
auto get = [&](function<bool(int,int)> f) -> long long {
vector<int> left(n, -1),right(n, n);
stack<int> sk;
for (int i = 0; i < n; ++i) {
while (!sk.empty() && f(a[sk.top()],a[i])) {
right[sk.top()] = i;
sk.pop();
}
if (!sk.empty()) left[i] = sk.top();
sk.push(i);
}
long long s = 0;
for (int i = 0; i < n; ++i) {
s += 1ll * (i - left[i]) * (right[i] - i) * a[i];
}
return s;
};
return get([&](int x,int y){return x < y;}) - get([&](int x,int y){return x > y;});
}
区间中不大于x的数的数目
在给定 𝑁 长的数组 {𝐴} 中进行 𝑄 次询问 [𝐿𝑖,𝑅𝑖] 区间中不大于 𝐻𝑖 的元素个数。
- 1 <= n <= 100000
- 1 <= ai <= 1e9
分析
我们用树状数组维护区间和,将数组 a 带着下标,按照值大小从小到大排序,再将每个询问,按照 h 值从小到大排序。然后我们遍历每个询问,对于当前的 h,将数组 a 中小于等于的 h 的数的下标 pos 进行 add(pos,1), 这个询问的答案就是 ask(r)-ask(l-1);
vector<int> calc(vector<int>& a, vector<vector<int>>& qs) {
int n = a.size(), m = qs.size();
vector<int> ans(m), tr(n);
auto add = [&](int c, int x) {
for (; c <= n; c += c & -c) tr[c - 1] += x;
};
auto ask = [&](int c) {
int s = 0;
for (; c; c -= c & -c) s += tr[c - 1];
return s;
};
vector<array<int,2>> v;
vector<array<int,4>> q;
for (int i = 0; i < n; ++i)
v.push_back({a[i], i + 1});
for (int i = 0; i < m; ++i)
q.push_back({qs[i][0], qs[i][1], qs[i][2], i});
sort(v.begin(), v.end(), [&](array<int,2> x, array<int,2> y){return x[0] < y[0];});
sort(q.begin(), q.end(), [&](array<int,4> x, array<int,4> y){return x[2] < y[2];});
for (int i = 0, j = 0; i < m; ++i) {
while (j < n && v[j][0] <= q[i][2])
add(v[j++][1], 1);
ans[q[i][3]] = ask(q[i][1]) - ask(q[i][0] - 1);
}
return ans;
}
树上路径异或和
给出 𝑛 个点的一棵树,每个点有各自的点权,多次询问两个点简单路径所构成点集的异或和。
输入格式 第一行两个数字 𝑛 和 𝑚 , 𝑛 表示点数,𝑚 表示询问次数 。
接下来一行 𝑛 个整数 𝑎1,𝑎2,…,𝑎𝑛 ,表示每个点的点权。
接下来 𝑛−1 行 , 每行两个整数 𝑢,𝑣 ,表示点 𝑢 和点 𝑣 之间存在一条边。
再接下来 𝑚 行,每行两个整数 𝑢,𝑣 ,表示询问点 𝑢 到点 𝑣 的简单路径所构成点集的异或和。
输出格式 输出 𝑚 行,对于每个询问,输出一行。
- 1 <= n,m <= 200000
- 1 <= ai <= 1e6
分析
现求出每个点到跟节点的路径异或值,则两个点的路径异或值等于两个节点到根节点的异或值异或上最近公共祖先。
void solve(){
cin >> n >> m;
vector<int> a(n),sum(n);
rd(a);
LCA g(n);
for(int i = 0; i < n-1; ++i){
cin>>x>>y;
x--,y--;
g.add_edge(x,y);
}
function<void(int,int)> dfs=[&](int u, int fa){
if(fa==-1) sum[u]=a[u];
else sum[u]=sum[fa]^a[u];
for (auto v : g.g[u]) {
if (v != fa) {
dfs(v, u);
}
}
};
dfs(0,-1);
g.complete();
while(m--){
cin>>x>>y;
x--,y--;
int u=g.lca(x,y);
int t=sum[x]^sum[y]^a[u];
cout<<t<<"\n";
}
}
思路2
可以统计该路径上每一位有多少个1,如果有奇数个,则异或和为1,否则为0,这种方法还可以扩展到一并解决路径与,路径或问题,例如对于或问题,如果路径上该位存在1,则结果的该位为1,否则为0,对于与问题,路径上该位1的个数等于路径上元素个数,则该位为1,否则为0.
维护 s[u][i] 表示节点u的第i位到根结点一共有多少个1.
则路径u,v上的第i位1的数目为 (设 t = lca(u, v))
s[u][i]+s[v][i] - 2 * s[t][i] + ((a[t] & (1 << i)) ? 1 : 0)
void solve(int tt) {
cin >> n >> m;
vector<int> a(n);
for (auto &x : a) cin >> x;
LCA g(n);
for(int i=1;i<n;++i){
cin>>x>>y;
x--,y--;
g.add_edge(x,y);
}
vector<vector<int>> s(n,vector<int>(20));
function<void(int,int)> dfs = [&](int u,int fa) {
if(fa==-1){
for(int i=0;i<20;++i){
if(a[u]&(1<<i)) s[u][i]=1;
else s[u][i]=0;
}
}else{
for(int i=0;i<20;++i)
s[u][i]=s[fa][i]+((a[u]&(1<<i))?1:0);
}
for(auto v:g.adj[u]){
if(v!=fa){
dfs(v,u);
}
}
};
dfs(0,-1);
g.build();
while(m--){
cin>>x>>y;
x--,y--;
int u=g.get_lca(x,y);
int p=0;
for(int i=0;i<20;++i){
if((s[x][i]+s[y][i]-((a[u]&(1<<i))?1:0))%2==1)p=p|(1<<i);
}
cout<<p<<"\n";
}
}
最小或值生成树
给出𝑛个点, 𝑚条边的无向图, 每条边连接𝑢,𝑣两个端点,边权为𝑤, 求图的生成树的最小代价。
在这道题中, 我们定义一棵生成树的代价为他所有边的边权按位或得到的值。
- 1 <= u,v <= 2e5
- n - 1 <= m <= 4e5
- 1 <= w <= 1e9
分析
贪心 + 并查集
从高位到低位,判断某一位能否取0,使用并查集判断是否是生成树。
假设我们前面确定了这些位构成的数位res,且当前是第k 位,我们假设当前位取0 ,那么什么样的边会会在我们的答案中呢,首先这个边边权v的第k位一定是0 ,否则一或会使这一位位1,由于后面的位不确定因此后面取什么都行,但是前面一定要符合我们前面的res即这条边或完res,第k位之前的位置和res中应该相同,不同的话代表这条边在前面贪心的时候就去除了,要判段能否生成树,直接判断最后这个图是否连通即可。
const int N = 2e5 + 5;
int f[N];
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
int n,m,x,y,k,q,res;
void solve(){
cin>>n>>m;
vector<array<int, 3>> a(m);
for(int i=0;i<m;++i){
cin>>a[i][0]>>a[i][1]>>a[i][2];
a[i]={x,y,k};
}
auto chk = [&](int k)->bool{
iota(f+1,f+n+1,1);
int x=res,cnt = 0;
for(int i=0;i<m;++i){
int t=(1<<k)-1;
t&=a[i][2];
t|=x;
if((a[i][2]>>k&1)==0&&t==(x|a[i][2])) {
f[find(a[i][0])]=find(a[i][1]);
}
}
for (int i=1;i<=n;++i){
if(i==f[i]) cnt++;
}
return cnt!=1;
};
for(int i=30;~i;--i){
if(chk(i)) res |= (1 << i);
}
cout << res << "\n";
}
统计子数组的数量
给定长度为n的数组a和k, 如果一个子数组和除以k的余数正好等于子数组长度,则称其为好子数组,统计好子数组的数量。
- 1 <= n <= 2e5
- 1 <= k, a[i] <= 1e9
分析
- 显然子数组长度小于k,因为模k的范围在[0,k-1]
根据条件:
(a[i] + a[i+1] + ,,, + a[j]) % k = j - i + 1
设 s 为 a 的前缀和数组,则上式变为:
(s[j] - s[i - 1]) % k = j - i + 1
即:
(s[j] - j) % k = (s[i - 1] - (i - 1)) % k
使用map统计即可,注意子数组长度要小于k。
long long countSubarrays(vector<int> &a, int k) {
int n = a.size();
vector<int> s(n + 1);
map<int, int> cnt;
for (int i = 0; i < n; ++i) {
s[i + 1] = (s[i] + a[i]) % k;
}
long long ans = 0;
for (int i = 0; i <= n; ++i) {
if (i >= k) cnt[((s[i-k] - i)%k + k)%k]--;
ans += cnt[((s[i] - i)%k + k)%k];
cnt[((s[i] - i)%k + k)%k]++;
}
return ans;
}
异或后最少逆序对数
给你一个有 𝑛 个非负整数组成的数组 𝑎 ,你需要选择一个非负整数 𝑥,对数组 𝑎 的每一个 𝑎𝑖 与 𝑥 进行异或后形成新的数组 𝑏,要求 𝑏 数组的逆序对个数最小,如果有多个 𝑥 满足条件,输出最小的 𝑥。
- 1 <= n <= 3e5
- 0 <= ai <= 1e9
分析
按位来确定x 的每一位选什么,每一位之间都是独立的,从高到低枚举每一位,如果当前位取1 会使逆序对数量减少就取1,从高位到低位依次确定即可
long long mergeSort(int l, int r, vector<int>& nums, vector<int>& tmp) {
if (l >= r) return 0;
int m = (l + r) / 2;
long long res = mergeSort(l, m, nums, tmp) + mergeSort(m + 1, r, nums, tmp);
int i = l, j = m + 1;
for (int k = l; k <= r; k++) tmp[k] = nums[k];
for (int k = l; k <= r; k++) {
if (i == m + 1) nums[k] = tmp[j++];
else if (j == r + 1 || tmp[i] <= tmp[j]) nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
res += m - i + 1; //如果是a[i] >= a[j],tmp[i] <= tmp[j] 改为tmp[i] < tmp[j]
}
}
return res;
}
long long reversePairs(vector<int>& nums) {
vector<int> tmp(nums.size());
return mergeSort(0, nums.size() - 1, nums, tmp);
}
void solve(){
rd(n);
vector<int> a(n), b;
rd(a);
b = a;
long long mn=reversePairs(a),t;
long long res=0;
for(int k=30;~k;--k){
res |= 1 << k;
for (int i = 0; i < n; ++i)
a[i] = (b[i] ^ res);
t = reversePairs(a);
if (t < mn) {
mn = t;
} else res ^= 1 << k;
}
cout << mn << " " << res << "\n";
}
方块消失的操作次数
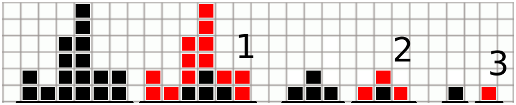
有𝑛堆方块,第𝑖堆方块由ℎ𝑖个方块堆积而成。具体可以看样例。
接下来拆方块。一个方块称为内部方块当且仅当他的上下左右都是方块或者是地面。否则方块就是边界方块。每一次操作都要把边界方块拿掉。
问多少次操作之后所有方块会消失。
- 1 <= n <+ 1e5
- 1 <= hi <= 1e9
分析
我们可以发现,操作最多执行 n/2次 ,因为每一次执行操作,都会消去两边的方块。 我们可以讨论,一个方块是因为变成了两边被消去,还是自己消去了。
对于中间的方块,如果左右的方块足够的多,那么最多 h[i]次操作后,这个方块就消去了。
如果一个方块被消去了后,下一步,它旁边的两个方块也会被消去。
所以我们可以考虑记录每个方块是被左边的方块消去,还是右边的方块消去,还是自己消去了。
dp1[i] 表示考虑左边,第 i个方块在 dp1[i] 次操作后被消去。
转移为 dp1[i]=min(dp1[i-1]+1,a[i]) 。
右边同理,取个 min 就是第 i 个方块消去的操作数。
最后记录下可以坚持最长时间的那个方块。
int calc(vector<int> &a) {
int n = a.size(), ans = 0;
vector<int> dp1(n + 1), dp2(n + 1);
for (int i = 0; i < n; ++i) dp1[i + 1] = min(dp1[i] + 1, a[i]);
for (int i = n - 1; ~i; --i) dp2[i] = min(dp2[i + 1] + 1, a[i]);
for (int i = 0; i < n; ++i) ans = max(ans, min(dp1[i + 1], dp2[i]));
return ans;
}
工作安排
有n项工作,每项工作话费一个单位时间,从时刻0开始,你每个时刻可以选择1-n项工作的任意一项工作完成。 每项工作有一个截止日期di, 完成该工作可以获得利润pi,在给定工作利润和截止时间下,能获得的最大利润是多少。
- 1 <= n <= 1e5
- 0 <= di, pi <= 1e9
反悔贪心
因为我们的工作的时间都为 1 ,所以我们可以直接贪心。用一个优先队列维护。
只要可以放,就放,如果放不了,就拿出利润最小的那个,比较最小的这个和当前工作的利润。
最后我们优先队列里面的,就是我们所选择的工作
/*
a[i][0]: 截止时间, a[i][1]:利润
*/
long long maxProfit(vector<vector<int>> &a) {
sort(all(a),[&](auto x, auto y){return x[0] < y[0];});
priority_queue<int, vector<int>, greater<int>> q;
for (int i = 0; i < (int)a.size(); ++i) {
if (a[i][0] <= 0) continue;
if (a[i][0] > q.size()) q.push(a[i][1]);
else if (a[i][1] > q.top()) {
q.pop();
q.push(a[i][1]);
}
}
long long ans = 0;
while (q.size()) {
ans += q.top(); q.pop();
}
return ans;
}
树上三角形数
给一个𝑛个节点的树, 三角果定义为一个包含3个节点的集合, 且他们两两之间的最短路长度𝑎, 𝑏, 𝑐能够构成一个三角形。
计算这棵树上有多少个不同的三角果
- 1 <= n <= 1e5
- 1 <= w <= 1e5
- 1 <= u, v <= n
1:树形DP
- 当三个点在树的一条路径上无解,其他情况均有解.
- 由于不在一条路径上因此必然存在一个中间结点分别与这些点相连,假设这个点和其他三个点相连的边权分别a,b,c,则a+b+b+c>a+c证明与权值路径权值无关了。
以点u 为中间点的方案数,这样的方案数由两部分构成:
- u 的两个不同的子树各选一个,非u 的子树里选一个这样是不会构成一条路径的
- u 的三个不同的子树各选一个,这样也不会构成一条路径
计算累乘和
- 给定数组a,计算(如下两个函数均可)
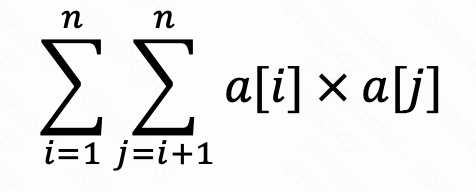
long long cal1(vector<long long> &a) {
long long s1 = 0, s2 = 0;
for (auto v : a) s1 += v, s2 += v * v;
return (s1 * s1 - s2) / 2;
}
long long cal2(vector<long long> &a) {
long long s1 = 0, s2 = 0;
for (auto &x: a) {
s1 = s1 + s2 * x;
s2 += x;
}
return s1;
}
- 给定数组a,计算(如下两个函数均可)
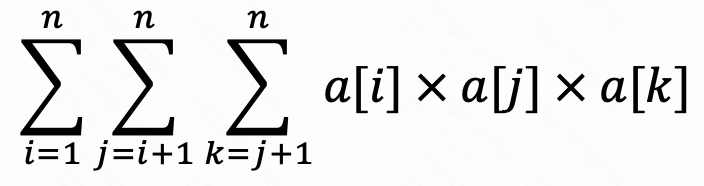
long long fun1(vector<long long> &a) {
long long s1 = 0, s2 = 0, s3 = 0;
for (auto v : a) s3 += v;
for (auto v : a) s1 += 1ll * v * v * v, s2 += 3ll * v * v * (s3 - v);
return (s3 * s3 * s3 - s1 - s2) / 6;
}
long long fun2(vector<long long> &a) {
long long s1 = 0, s2 = 0, s3 = 0;
for (auto &x: a) {
s3 = s3 + s2 * x;
s2 = s2 + s1 * x;
s1 = s1 + x;
}
return s3;
}
long long cal1(vector<long long> &a) {
long long s1 = 0, s2 = 0;
for (auto v : a) s1 += v, s2 += v * v;
return (s1 * s1 - s2) / 2;
}
long long cal2(vector<long long>&a) {
long long s1 = 0, s2 = 0, s3 = 0;
for (auto v : a) s3 += v;
for (auto v : a) s1 += 1ll * v * v * v, s2 += 3ll * v * v * (s3 - v);
return (s3 * s3 * s3 - s1 - s2) / 6;
}
void solve(){
cin>>n;
vector<vector<int>> g(n);
f0(n-1){
rd(x,y,k);
x--,y--;
g[x].push_back(y);
g[y].push_back(x);
}
long long c=0;
vector<long long> s(n);
function<void(int,int)> dfs=[&](int u,int fa){
s[u]=1;
vector<long long> a;
for(auto&v:g[u]){
if(v!=fa){
dfs(v,u);
a.push_back(s[v]);
s[u]+=s[v];
}
}
int m=a.size();
if(m>=2) c+=cal1(a) * (n-s[u]);
if(m>=3) c+=cal2(a);
};
dfs(0,-1);
wt(c,'\n');
}
数学
如果将当前点u 去除掉我们可以得到好几颗子树,问题转化为从这些树中选三棵树每个每棵树选一个结点,设每个树的节点数为s[i], 也就是我们可以枚举其中一个点,然后保证这个点前面的递增,后面的递减即可,也就是等价于我们求到了u 这个点对于已经出现的点作为左半部分,当前枚举的作为u,未枚举到的作为右半部分,因此就可以O(n)的求了。
vector<long long > s(n);
long long c = 0;
function<void(int,int)> dfs=[&](int u,int fa){
s[u]=1;
for(auto&v:g[u]){
if(v!=fa){
dfs(v,u);
c += (s[u] - 1) * s[v] * (n - s[u] - s[v]);
s[u] += s[v];
}
}
};
dfs(0,-1);
环上分段和的最大公约数
环上有𝑛个正整数。你能将环切成𝑘段,每段包含一个或者多个数字。
对于一个切分方案,优美程度为每段数字和的最大公约数,你想使切分方案的优美程度最大,对于𝑘=1,2,…,𝑛输出答案。
- 1 <= n <= 2000
- 1 <= a[i] <= 5e7
分析
- g 为数组总和的因子,可以枚举 sum 的因子。
- 如果一个因子可以是切成k段的结果,那么它也可以是切成k-1段的结果
vector<long long> maxKsegmentGCD(vector<int> &a) {
int n = a.size();
vector<long long> s(n + 1), ans(n);
for (int i = 0; i < n; ++i) {
s[i + 1] = s[i] + a[i];
}
auto cal = [&](long long x) {
map<long long, int> mp;
int cot = 0;
for (int i = 1; i <= n; i++) {
mp[s[i] % x]++;
cot = max(cot, mp[s[i] % x]);
}
ans[cot - 1] = max(ans[cot - 1], x);
};
int sq = sqrt(s[n]);
for (int i = 1; i <= sq; ++i) {
if (s[n] % i == 0) {
cal(i);
cal(s[n] / i);
}
}
for (int i = n - 2; ~i; --i) {
ans[i] = max(ans[i + 1], ans[i]);
}
return ans;
}
字典序最小
从序列 𝑀 个数中顺序选出 𝑁 个不同的数, 使得这 𝑁 个数的字典序最小。 其中 1≤𝑎𝑖≤𝑁, 数据保证 [1,𝑁] 范围内每个数至少出现一次。
让你找一个子序列,为 N 的排列,使得字典序最小,保证至少存在一个排列
- 1 < n <= m <= 1e6
单调栈
顺序枚举,对于a[i],如果a[i]已经在栈中,不做处理,否则,我们弹出所有大于a[i]的数,来保证字典序最小 但需要注意,弹出的数需要保证后面还有这个数,不然的话就不满足每个数都出现一次了。
/*
0 <= a[i] <= n - 1
*/
vector<int> minLexicographicalPerm(vector<int> &a, int n) {
int m = a.size();
vector<int> p(n), s, st(n);
for (int i = 0; i < m; ++i) {
p[a[i]] = i;
}
for (int i = 0; i < m; ++i) {
if (st[a[i]]) continue;
while (s.size() && s.back() > a[i] && p[s.back()] > i) {
st[s.back()] = 0;
s.pop_back();
}
st[a[i]] = 1;
s.push_back(a[i]);
}
return s;
}
好序列
有一个长为𝑛的序列𝐴1,𝐴2,…,𝐴𝑛。定义一个序列{𝐴}是好的, 当且仅当他的每一个子区间[𝑙,𝑟]满足,至少存在一个元素𝑥仅出现了一次。
- 1 <= n <= 2e5
- 1 <= a[i] <= 1e9
启发式合并
bool isGoodSequence(vector<int> &a) {
int n = a.size();
vector<int> pre(n + 1, -1), nxt(n + 1, n + 1);
map<int, int> mp;
for (int i = 1; i <= n; ++i) {
pre[i] = mp[a[i - 1]];
nxt[mp[a[i - 1]]] = i;
mp[a[i - 1]] = i;
}
function<bool(int, int)> split = [&](int l, int r) -> bool {
if (l >= r) return 1;
int x = l, y = r;
while (x <= y) {
if (pre[x] < l && r < nxt[x]) return split(l, x - 1) && split(x + 1, r);
if (pre[y] < l && r < nxt[y]) return split(l, y - 1) && split(y + 1, r);
x++, y--;
}
return 0;
};
return split(1, n);
}
区间和
长度为n的数组A, 给出q个提示,第i个提示是A中L到R连续元素的区间和,能否根据q个提示知道数组所有元素的和?
分析
对于给定的区间和,我们考虑前缀和。
给定区间 [l,r] 的和,相当于告诉了我们 s[r] - s[l - 1]的值,如果我们知道了其中一个数的值,那么另外的一个值也可以得到。
我们可以通过给定的关系,得到 s[n] 的值。所以我们直接用一个并查集维护即可。
struct DSU {
public:
DSU() : _n(0) {}
explicit DSU(int n) : _n(n), parent_or_size(n, -1) {}
int merge(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
int x = get(a), y = get(b);
if (x == y) return x;
if (-parent_or_size[x] < -parent_or_size[y]) std::swap(x, y);
parent_or_size[x] += parent_or_size[y];
parent_or_size[y] = x;
return x;
}
bool same(int a, int b) {
assert(0 <= a && a < _n);
assert(0 <= b && b < _n);
return get(a) == get(b);
}
int get(int a) {
assert(0 <= a && a < _n);
if (parent_or_size[a] < 0) return a;
return parent_or_size[a] = get(parent_or_size[a]);
}
int size(int a) {
assert(0 <= a && a < _n);
return -parent_or_size[get(a)];
}
std::vector<std::vector<int>> groups() {
std::vector<int> leader_buf(_n), group_size(_n);
for (int i = 0; i < _n; i++) {
leader_buf[i] = get(i);
group_size[leader_buf[i]]++;
}
std::vector<std::vector<int>> result(_n);
for (int i = 0; i < _n; i++) {
result[i].reserve(group_size[i]);
}
for (int i = 0; i < _n; i++) {
result[leader_buf[i]].push_back(i);
}
result.erase(
std::remove_if(result.begin(), result.end(),
[&](const std::vector<int>& v) { return v.empty(); }),
result.end());
return result;
}
private:
int _n;
// root node: -1 * component size
// otherwise: parent
std::vector<int> parent_or_size;
};
bool check(int n, vector<array<int, 2>> &Q) {
DSU dsu(n + 1);
for (auto& [l, r]: Q) {
dsu.merge(l - 1, r);
}
if (dsu.same(0, n)) return 1;
return 0;
}
最大权值和划分
对于一段序列,这段序列的权值定义为最大值与最小值之差,给定数组a,可以将其划分为任意连续的序列,求出数组每一段权值求和的最大值
- 1 <= n <= 1e6
- -1e9 <= a[i] <= 1e9
分析
最优解中,数组分成的每一段序列内部都是单调的,这样不会对最终的结果值造成损失。
- dp[i][0]: 第i个数在下降序列中的最大值
- dp[i][1]: 第i个数在上升序列中的最大值
当遍历到a[i]时,如果a[i]>a[i-1]: 讨论a[i-1]在上升序列或下降序列中,可得dp[i][1]=max(dp[i-1][0],dp[i-1][1]+a[i]-a[i-1]) dp[i][0] = max(dp[i-1][0],dp[i-1][1])
long long maxWeightSum(vector<int> &a) {
int n = a.size();
vector<vector<long long>> dp(n, vector<long long>(2));
for (int i = 1; i < n; ++i) {
if (a[i] > a[i - 1]) {
dp[i][1] = max(dp[i - 1][0], dp[i - 1][1] + a[i] - a[i - 1]);
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
} else {
dp[i][0] = max(dp[i - 1][0] + a[i - 1] - a[i], dp[i - 1][1]);
dp[i][1] = max(dp[i - 1][0], dp[i - 1][1]);
}
}
return max(dp[n - 1][0], dp[n - 1][1]);
}
acwing
平均值大于k的最长子数组长度
长度为n的数组A, 请你找到一个序列 a 的连续子序列 a[l], a[l+1], …, a[r],要求:
- a[l]+a[l+1]+,,,+a[r] > 100 * (r - l + 1)
-
子数组长度尽可能大
- 1 <= n <= 1e6
- 0 <= a[i] <= 5000
求子数组的最大可能长度.
分析
s[r] - s[l - 1] > 100 (r - l + 1)
即: s[r]-s[l-1]-100(r-l+1) > 0
设 s1 为 a[i] - 100 数组的前缀和, 即 s1[r] > s1[l] (l < r) 求 r - l 的最大值。
如果 i < j 同时 s[i] <= s[j] 则,s[j] 不会成为任意大于j的最小的l,所以可以维护一个单调递减的栈,每次对栈进行二分。
代码
int lengthestSubArray(vector<int> &a, int k) {
int n = a.size(), ans = 0;
vector<long long> s(n + 1);
for (int i = 0; i < n; ++i)
s[i + 1] = s[i] + (a[i] - k);
vector<int> sk;
for (int i = 0; i <= n; ++i) {
if (sk.empty() || s[sk.back()] > s[i]) {
sk.push_back(i);
} else {
int l = 0, r = sk.size() - 1, res = -1;
while (l <= r) {
int mid = (l + r) / 2;
if (s[sk[mid]] < s[i]) {
res = mid;
r = mid - 1;
} else l = mid + 1;
}
if (res != - 1)
ans = max(ans, i - sk[res]);
}
}
return ans;
}
O(n)算法
对原数组作减k操作,设s为新数组的前缀和,问题转化为: 在s数组中找到一对i,j 使得 s[j] > s[i] 且 (j - i) 最大。
- 对于一个i,如果i左侧有小于或等于s[i]的元素,那么i不可能成为最优答案中的i。
- 对于一个j,如果j右侧有大于或等于s[j]的元素,那么j不可能成为最优答案中的j。
设 lmn[i]:表示 s[0],…s[i]中的最小值,rmx[j]: 表示s[j]…s[n]中的最大值。
显然,lmn 和 rmx 都是单调不增序列。
从前向后遍历两个数组,如果 lmn[i] >= rmx[j],则执行 i++, 如果 lmn[i] < rmx[j], 更新 ans, 同时执行 j++;
int lengthestSubArray(vector<int> &a, int k) {
int n = a.size();
vector<long long> s(n + 1);
for (int i = 0; i < n; ++i)
s[i + 1] = s[i] + (a[i] - k);
auto lmn = s, rmx = s;
for (int i = 1; i <= n; ++i)
lmn[i] = min(lmn[i - 1], s[i]);
for (int i = n - 1; i >= 0; --i)
rmx[i] = max(rmx[i + 1], s[i]);
int i = 0, j = 0, ans = 0;
while (i <= n && j <= n) {
if (lmn[i] < rmx[j]) {
ans = max(ans, j - i);
j = j + 1;
} else i = i + 1;
}
return ans;
}
所有子数组平均数之和
给定一个数组,求出这段数组中所有子数组的平均数之和。
答案对1e9+7取模,假设答案的最简分数表示为a/b,你需要输出最小的非负整数x,使得x*b与a模(1e9+7)同余。
- 1 <= n <= 1e6
- 0 <= a[i] <= 1e9
分析
对于不同长度的子区间,每个元素贡献的次数
a[1] a[2] a[3] a[4] a[5] a[6] a[7]
l = 1 1 1 1 1 1 1 1
l = 2 1 2 2 2 2 2 1
l = 3 1 2 3 3 3 2 1
l = 4 1 2 3 4 3 2 1
l = 5 1 2 3 3 3 2 1
l = 6 1 2 2 2 2 2 1
l = 7 1 1 1 1 1 1 1
对于长度l=1,2,…,n分别考虑 当l=1时,所有长度为1的子数组和为s[n]-s[0],记作sum[1]; 当l=2时,a[1]和a[n]贡献一次,a[2]…a[n-1]贡献两次 … 可得递推关系,见代码。
最后对于每个长度进行累加和, a/b = a* pow(b,mod-2)
int calSubArrayMeanSum(vector<int> &a) {
int n = a.size(), mod = 1e9 + 7;
vector<long long> p(n + 1), s(n + 1);
for (int i = 0; i < n; ++i)
p[i + 1] = (p[i] + a[i]) % mod;
for (int l = 1; l <= n; ++l) {
if (l <= (n + 1) / 2) s[l] = (s[l-1] + p[n + 1 - l] - p[l - 1]) % mod;
else s[l] = s[n + 1 - l];
}
auto qp = [&](long long x, long long y) {
long long c = 1, t = x;
for (; y; y >>= 1) {
if (y & 1) c = c * t % mod;
t = t * t % mod;
}
return c;
};
long long ans = 0;
for (int l = 1; l <= n; ++l) {
ans = (ans + s[l] * qp(l, mod - 2)) % mod;
}
return (ans + mod) % mod;
}
均值大于等于k的子数组数目
给定长度为n的数组k,求有多少对子数组,其平均值大于等于k。
- 1 <= n <= 2e5
- 1 <= k <= 1e9
- 1 <= a[i] <= 1e9
分析
首先对所有数减去k,设其前缀和数组为s,问题转化为有多少对l,r使得s[r]-s[l-1]>=0, 用树状数组对s求有多少个顺序对。
long long countSubArraysK(vector<int> &a, int k) {
int n = a.size();
vector<long long> s(n + 1), tr(n + 1);
for (int i = 0; i < n; ++i) {
s[i + 1] = s[i] + (a[i] - k);
}
auto add = [&](int x) {
for (; x <= n + 1; x += x & -x) tr[x - 1] += 1;
};
auto ask = [&](int x) {
int res = 0;
for (; x > 0; x -= x & -x) res += tr[x - 1];
return res;
};
auto v = s;
sort(v.begin(), v.end());
v.erase(unique(begin(v), end(v)), end(v));
long long ans = 0;
for (int i = 0; i <= n; ++i) {
int p = lower_bound(v.begin(), v.end(), s[i]) - v.begin() + 1;
ans += ask(p); //如果是大于k的数目,改为ask(p-1)
add(p);
}
return ans;
}
数对
给定长度为n的数列和两个整数x,y. 求有多少个数对 l, r, 满足
- 1 <= l <= r <= n
-
a[l] + a[l+1] + ,,, + a[r] <= x + y * (r - l + 1)
- 1 <= n <= 2e5
- -1e9 <= a[i] <= 1e9
- -1e12 <= x, y <= 1e12
解析
另 b[i] = a[i] - y, 设b的前缀和数组为s,上述公式变为 s[r] - s[l - 1] <= x 可以在值域上维护一个树状数组,维护每个前缀和数值的个数和。遍历右边端点r进行累加。
long long countPairs(vector<int> &a, long long x, long long y) {
int n = a.size();
vector<long long> s(n + 1), v;
for (int i = 0; i < n; ++i) {
s[i + 1] = s[i] + a[i] - y;
}
for (int i = 0; i <= n; ++i) {
v.push_back(s[i]);
v.push_back(s[i] - x);
}
sort(v.begin(), v.end());
v.erase(unique(begin(v), end(v)), end(v));
vector<long long> tr(v.size() + 1);
auto add = [&](int x) {
for (; x <= (int)tr.size(); x += x & -x) tr[x - 1] += 1;
};
auto ask = [&](int x) {
int res = 0;
for (; x > 0; x -= x & -x) res += tr[x - 1];
return res;
};
auto get = [&](long long x) {
return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
};
long long ans = 0;
for (int i = 0; i <= n; ++i) {
ans += i - ask(get(s[i] - x) - 1);
add(get(s[i]));
}
return ans;
}
解法2
可以直接用平衡树求 小于 s[r] - x 的l有多少个。 需要一个支持下表访问的multiset。
struct mulset {
// mulset 模板
};
long long countPairs(vector<int> &a, long long x, long long y) {
int n = a.size();
vector<long long> s(n + 1), v;
for (int i = 0; i < n; ++i) {
s[i + 1] = s[i] + a[i];
}
mulset<long long, less<long long>> st;
st.insert(0);
long long ans = 0;
for (int i = 1; i <= n; ++i) {
ans += i - st.order_of_key(s[i] - x);
st.insert(s[i]);
}
return ans;
}
错位排列
求n封信的错位排列,n <= 1e9
分析
打表,分成1000个块
int calc(int n, int mod) {
const ll L[1005] = {1, 102701088, 981992119, 649506278, 627764250, 645138131, 564166077, 806340002, 832288921, 136850473, 824182295, 485486901, 362408075, 230615570, 207753791, 746724534, 218498984, 781396008, 329051776, 323681136, 933713113, 55283981, 981439786, 825501686, 138007547, 342331196, 289391657, 825412508, 187428012, 141252153, 474482547, 469345798, 143251826, 921539885, 480488466, 371921930, 231080468, 854891028, 745269989, 838798600, 930651136, 166822045, 373911211, 895972398, 171482268, 451712763, 958587080, 752005616, 988795902, 572897149, 251064654, 321585864, 511830767, 631659409, 144463808, 390942798, 102930668, 688993450, 106803430, 736094471, 637937211, 67539869, 144102058, 272682427, 403369349, 888623609, 858619719, 775950042, 15647887, 791153158, 229643390, 418285941, 386152375, 926363365, 39644216, 774661798, 40160713, 396825904, 995555017, 857467965, 307311871, 322363308, 558471991, 849546729, 702107511, 610253183, 836510216, 371849840, 951720735, 611938075, 448853213, 916443128, 719396272, 62461078, 829557374, 360973550, 28257290, 54217657, 360608813, 40750050, 322273426, 994158933, 169297167, 816619563, 578752871, 360557868, 348588664, 773488558, 383760456, 253636234, 398890147, 995241802, 479632402, 110532161, 700282646, 282610478, 140824426, 295951236, 857609436, 760044280, 194914852, 443829327, 876081218, 524150684, 964703318, 503814959, 3721180, 438887824, 780454157, 618807385, 884947442, 765009239, 49016763, 277882991, 686914924, 394281833, 9292295, 180115281, 827376728, 884535605, 154199209, 244167252, 56875341, 100252189, 949590677, 930382776, 186095009, 915325731, 487153268, 999188962, 881788023, 26750235, 843660084, 825675146, 480858823, 814808681, 562764753, 388965635, 868321452, 793774212, 389699639, 696033877, 824165623, 729212269, 903496758, 13694466, 125127133, 802590026, 78636716, 991813302, 733217502, 340792204, 163694105, 729692726, 66435775, 124648772, 579867155, 90056478, 540654765, 368988366, 601739182, 416701437, 445350912, 616246755, 591423736, 392220359, 536341336, 964430099, 531887312, 559587397, 372305477, 718309972, 926423310, 42000939, 639265371, 28855165, 677697221, 103286437, 484351515, 607563402, 213823357, 872307731, 372467702, 126282642, 345280228, 984769112, 717461814, 487124435, 757943584, 562591933, 713959988, 970592690, 854865267, 918201995, 777177924, 466044211, 718369887, 595693165, 48090102, 581617266, 498202615, 215303046, 391636760, 679592087, 66223098, 332910243, 554427583, 437417932, 759812013, 129290794, 196342945, 383628392, 474049070, 499347791, 729105951, 715068952, 708424167, 417690245, 981761551, 100358731, 324300550, 448815874, 976802967, 355804045, 868183507, 299712064, 548578229, 311019993, 739059075, 589778521, 154001751, 348119666, 539751867, 574158273, 788685196, 791279153, 624440017, 961214770, 231405777, 245724014, 974475946, 275533551, 845138374, 157087033, 736460202, 470540891, 871607895, 745317906, 387858087, 242782878, 540773759, 747935865, 859460625, 228821922, 723487306, 468917247, 724324069, 476378557, 770600635, 250470252, 467881322, 300357120, 676487052, 462154550, 311697536, 428812399, 450648083, 778076329, 786255939, 765849472, 257531902, 721767280, 176563389, 175749454, 732296574, 298120095, 155448833, 898525679, 85049317, 968406065, 598680559, 395844987, 900957536, 579095485, 429212998, 509837298, 853242300, 922588922, 68856856, 283770130, 367927849, 522655659, 690757326, 912348796, 30049334, 131745858, 137674199, 142648551, 600945940, 449239819, 971346692, 670051193, 737038504, 865244796, 723942192, 610008278, 752447580, 905516484, 656581760, 91825933, 94577421, 283622038, 849585022, 102547070, 323875198, 420318614, 779228990, 786063302, 988963335, 164868451, 617165552, 905989955, 6391586, 421243975, 739350754, 362563274, 347053973, 576876354, 394564599, 99117090, 128327758, 435476476, 728083087, 600210704, 507934245, 259790921, 404690060, 506558658, 328287279, 237225611, 503709458, 465806023, 631623755, 594216496, 370047171, 737911496, 151018717, 113095146, 128457419, 880656919, 253566817, 184922743, 223563582, 252228570, 266519182, 876803028, 194040840, 997525075, 847784903, 464959842, 820144401, 163870432, 885252811, 688921891, 193947871, 21626547, 958041818, 727618041, 842250, 378454511, 13965056, 409131285, 863668228, 688461155, 117468217, 29814411, 531114442, 25589724, 254857335, 305168698, 82358069, 445751007, 411378564, 381536877, 933633977, 702145011, 687788151, 558820531, 829116226, 956393708, 805941568, 178263460, 900513582, 928732556, 122675017, 699849090, 47406175, 823318492, 754665638, 211464760, 533047638, 354855600, 56228475, 889527707, 89342482, 925349438, 352847983, 184575152, 162590565, 402474435, 69430220, 53717597, 499227545, 727117226, 389321885, 505427812, 689377848, 739141890, 851692242, 36961625, 686678173, 898151821, 341673172, 603840769, 314510027, 988116160, 292613275, 643463284, 987869224, 86904847, 297170813, 210607265, 125056557, 522472396, 56762503, 268825217, 657107621, 541102843, 405700172, 597167891, 34546238, 219235406, 288417029, 32306949, 6461506, 75810449, 187271994, 958412125, 923423574, 174329621, 323435423, 134419822, 86333313, 623634963, 819270744, 708774997, 864549168, 184708668, 808590464, 146071060, 499126069, 957779045, 733872556, 966196700, 801414729, 725378301, 475620410, 387306873, 921714578, 242623264, 487532712, 808421122, 796370648, 958262856, 56469791, 969427220, 906919416, 154436480, 771008169, 213577806, 468899710, 432769540, 870216603, 51442776, 12237969, 675843097, 34760677, 396204835, 176554723, 414179745, 790590914, 225772745, 567888121, 233151084, 152099332, 751227942, 46458325, 674788795, 790702570, 489845612, 581347156, 369818845, 15615037, 545967596, 103309552, 389860753, 719815661, 91664918, 301486883, 791845156, 955359050, 779856088, 44321908, 489350942, 644787192, 55206524, 633954632, 598404606, 901413642, 149686777, 700529992, 579052159, 565835015, 118847032, 867926968, 97589652, 729449902, 6064412, 401641163, 221211052, 518280890, 609694504, 63376104, 428801015, 700687934, 839096293, 114480112, 98459976, 876598556, 693812577, 98592091, 74920668, 224533248, 721549085, 970958369, 117610907, 347169727, 961003451, 478317111, 306883443, 64544225, 131097347, 11349170, 278833977, 412976440, 72910913, 191951439, 443412274, 570830448, 149888564, 988209678, 265614314, 152910522, 327272434, 752186716, 718262387, 133171332, 618790917, 53007885, 650106860, 422603955, 660805266, 503088446, 947525042, 635064394, 781322580, 447596506, 461800272, 848471668, 994245679, 40661679, 298018995, 657681727, 690493596, 651688259, 263114315, 625223306, 676841440, 338387319, 196183571, 174468756, 736236357, 307800572, 232333370, 680437177, 135268337, 94262259, 770243628, 584612051, 457097995, 573631136, 676573626, 577189995, 357633724, 491460743, 183599737, 710075282, 650365986, 746259674, 604986809, 757555557, 422575560, 51985410, 521611328, 59618475, 551225407, 521615404, 187849667, 486159922, 34760970, 710709955, 68171314, 939418137, 95539701, 729618083, 669334209, 91219418, 557643173, 582111925, 687457420, 775098981, 898616827, 603014921, 576780933, 893649850, 278152475, 203936502, 158338523, 977791269, 446417809, 499158883, 632455012, 596308186, 941696136, 698436253, 417623410, 894434290, 88077857, 914667320, 174322412, 969149294, 488979053, 19360531, 551406263, 73316989, 119956407, 847556159, 152414193, 15968687, 103264601, 880429710, 963452539, 316525653, 363527941, 565064060, 950456028, 875759441, 715221164, 333793105, 401872114, 42564126, 757147276, 585211132, 442500985, 949069261, 480460278, 447188779, 95227949, 994464164, 991942192, 333697951, 954980943, 178264106, 915367944, 150152513, 159044774, 181427295, 574673435, 164721975, 713579760, 522067888, 820113517, 404395270, 459838540, 175975086, 139109834, 531733674, 414553797, 17880902, 333986091, 579797877, 473169256, 788793995, 820866545, 948934214, 702467776, 314706865, 200780118, 211722873, 818674597, 528967798, 962265651, 515626105, 517981574, 768844703, 208784939, 664133726, 950847823, 177984668, 618427638, 717694718, 803357822, 751009820, 376612251, 691294576, 756271819, 211958024, 543942422, 197601451, 947893174, 309384913, 234460299, 452161730, 934679817, 650662942, 815852027, 812802047, 356180431, 780228545, 435897276, 31308092, 440411884, 218696216, 960164158, 154837346, 38316616, 962683091, 10606516, 552913767, 606494944, 316850320, 364888293, 94513584, 294155313, 501476310, 567610607, 822846632, 345872164, 516729942, 86574506, 220854491, 306148897, 929299169, 423969930, 125383915, 782132070, 667142092, 184842982, 481533802, 770543419, 878646494, 831895011, 575605965, 258561151, 39657326, 430961569, 849881078, 746427504, 480064563, 889303958, 963974981, 898310091, 746327924, 259305179, 267660342, 677796098, 560277115, 821037552, 72328802, 987119561, 377654637, 943684790, 632757568, 205829180, 3053655, 972289649, 395572519, 686813938, 609494839, 670784224, 705101053, 125163116, 202791269, 973029224, 28732033, 671770693, 630644805, 159448906, 192678133, 109528400, 542246848, 655276546, 350104791, 339661876, 811164546, 523433471, 913806489, 681290582, 320368010, 184855330, 466289530, 539681423, 790812019, 439374936, 461375205, 209088494, 867942331, 476008696, 18780215, 520734953, 750036412, 738072355, 952000246, 218649908, 160577387, 619720649, 562085462, 705486526, 22383103, 435748056, 819636314, 443829864, 351469219, 609164310, 111175592, 458416215, 63207979, 361128966, 817329481, 102726115, 688721174, 890414414, 99411932, 154717014, 44860063, 594743835, 900253101, 909158470, 817994577, 933285383, 464087273, 753073278, 999122550, 47465597, 951314008, 645783065, 316910697, 132946886, 383979285, 877774703, 517164631, 915986682, 331585939, 797408571, 624813671, 280636995, 170701415, 241387050, 696417434, 877840727, 256789690, 280434105, 927498321, 737288545, 520988669, 56826112, 685369539, 131583290, 719116784, 880238527, 482685016, 605351713, 993736121, 206881884, 811177899, 141317021, 3335944, 585698084, 682073860, 531426532, 276682441, 663644092, 689352730, 727852213, 746814819, 184143102, 428872926, 481695945, 218798350, 773608829, 473333947, 116103680, 655473387, 968076915, 86359458, 334781593, 717843074, 37035206, 134224352, 615288312, 340221393, 901599799, 264410783, 458906778, 806163165, 144415001, 56614453, 868868442, 454860259, 357904502, 762927538, 930045611, 768284771, 349135872, 375939507, 726718378, 896128453, 285627228, 668118735, 198917702, 624766601, 425203890, 855319974, 767663944, 540515728, 317375305, 348158328, 809965487, 392140412, 661597068, 984537252, 670848732, 400577109, 640781611, 437555867, 116644591, 178175499, 738119236, 6174353, 123815837, 977632075, 118428592, 215737742, 626057315, 535141995, 511506338, 204569608, 676562680, 681205105, 252631325, 34192646, 396906487, 914120126, 14839562, 611781105, 176769488, 320106189, 532057908, 152225254, 960210904, 402182971};
long long X = 1e6, ans = L[n / X];
for (ll i = n / X * X + 1; i <= n; i++) {
ans = ans * i % mod;
if (i % 2 == 0) ans = (ans + 1) % mod;
else ans = (ans + mod - 1) % mod;
}
return ans;
}
其它
统计排列的mex值
给定一个0-(n-1)的排列组成的数组,对于i从1到n,统计MEX值等于i的子数组的数目。
MEX值 是数组中未出现的最小非负整数。例如对于数组[2,0,1],MEX值为1的有 [2,0]和[0],MEX值为2的有[0,1],MEX值为3的有[2,0,1]。
- 1 <= n <= 3e5
分析
假设某个子数组的MEX值为k,那么该子数组包含0-(k-1)的所有数,但不包含k. 包含0-(k-1)的最小数组为[l,r],如果k的下标在[l,r]内,则不存在MEX值为k的子数组,因为选择0-(k-1)必须把k也选中。如果 k的下标idx,小于l, 则左边界从idx+1到l,右边界从r到(n-1)都满足条件,同时更新l为idx,同理可分析idx>r的情况。从0-n维护[l,r]即可。
vector<long long> countPermulationMEX(vector<int> &a) {
int l, r, n = a.size();
vector<int> p(n);
for (int i = 0; i < n; ++i) {
p[a[i]] = i;
if (a[i] == 0) l = i, r = i;
}
vector<long long> ans(n);
ans[n - 1] = 1;
for (int i = 0; i < n - 1; ++i) {
int k = p[i + 1];
if (l > k) {
ans[i] = (n - r) * 1ll * (l - k);
l = k;
} else if (r < k) {
ans[i] = (l + 1ll) * (k - r);
r = k;
}
}
return ans;
}
交换后最小化最值差
两个长为n的数组a,b,每次操作可以选择一个i,交换a[i],b[i],可以操作任意次,求能取得的 a_max-a_min的最小值。
- 1 <= n <= 2e5
- 1 <= a[i], b[i] <= 1e9
int minDiffSwaps(vector<int> &a, vector<int> &b) {
int n = a.size();
vector<pair<int,int> > c(n);
for (int i = 0; i < n; ++i) {
c[i] ={min(a[i],b[i]), max(a[i],b[i])};
}
sort(c.begin(), c.end());
multiset<int> s;
for (int i = 0; i < n; ++i) {
s.insert(c[i].first);
}
int ans = *(s.rbegin()) - *(s.begin());
for (int i = 0; i < n; ++i) {
s.erase(c[i].first);
s.insert(c[i].second);
ans = min(ans, *(s.rbegin()) - *(s.begin()));
}
return ans;
}
不相交子数组数目
长为n的数组A,求有多少个不相交的区间 [a,b] 和 [c,d], 1 <= a <= b < c <= d <= n, 满足 A[a..b] 和 A[c..d]两个子数组中不存在相同元素。
- 1 <= n <= 1000
- 1 <= A[i] <= 1e9
分析
https://discuss.codechef.com/t/chsgments-editorial/12767
template <class T>
struct Discrete {
vector<T> xs;
Discrete(const vector<T>& v) {
xs = v;
sort(xs.begin(), xs.end());
xs.erase(unique(xs.begin(), xs.end()), xs.end());
}
int get(const T& x) const {
return lower_bound(xs.begin(), xs.end(), x) - xs.begin();
}
inline int operator()(const T& x) const { return get(x); }
T operator[](int i) { return xs[i]; }
int size() const { return xs.size(); }
};
int count_non_intersec_seg(vector<int> &a) {
Discrete<int> v(a);
for(int &x:a)
x=v(x);
int n=a.size();
vector<vector<int>> p(n);
for (int i = 0; i < n; ++i) {
p[a[i]].push_back(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
set<int> b{i - 1, n};
vector<int> vis(n);
int tot = (n - i) * (n - i + 1) / 2;
for (int j = i; j < n; ++j) {
if (vis[a[j]]) {
ans += tot;
continue;
}
vis[a[j]] = 1;
for (int x : p[a[j]]) {
auto it = b.lower_bound(x);
int r = *it, l = *prev(it);
tot -= (x - l) * (r - x);
b.insert(x);
}
ans += tot;
}
p[a[i]].erase(p[a[i]].begin());
}
return ans;
}
删除子数组的方案数
给定数组A。计算有多少种不同的方案能从该序列中删去一个非空的子数组,使得剩余的数组非空且严格递增。
- 1 <= n <= 1e5
- -1e9 <= a[i] <= 1e9
分析
long long countDelWays(vector<int> &a) {
int n = a.size(), r = n;
a.insert(a.begin(), INT_MIN);
long long ans = 0;
while (r - 1 >= 1 && a[r] > a[r - 1]) r--;
ans = n - max(1, r - 1);
for (int l = 1; l < n; l++) {
if (not (a[l - 1] < a[l])) break;
while (r <= n and not (a[l] < a[r])) r++;
ans += n - max(l + 1, r - 1) + 1;
}
return ans;
}
最大异或值的最小x
给定一个整数A,选择两个整数(X,Y),使1<=X,Y<=A,使它们的xor值最大。 如果有多个(X, Y);选择一个最小的X。
- 1 <= A <= 1e9
vector<int> maxXorMinX(int n) {
if (n == 1) return {1, 1};
int x = 32 - __builtin_clz(n), k = (1 << x) - 1;
return k == n ? vector<int>{1, n - 1} : vector<int>{k ^ n, n};
}
第n个二进制表示是回文串的数
给定整数n,找到第n个二进制表示是回文串的数
- 1 <= n <= 2e4
int nth_palin(int n) {
long long p = 1, ans = 0;
int l = 0, sum = 1;
while(1) {
l++;
if(sum + p > a) break;
sum += p;
l++;
if(sum + p > a) break;
sum += p;
p <<= 1;
}
int bits[l]{};
bits[0] = bits[l - 1] = 1;
int mid = l >> 1, diff = a - sum;
for(int i = 0; diff && i < mid; i++) {
bits[mid - i - !(l & 1)] = bits[mid + i] = diff & 1;
diff >>= 1;
}
p = 1;
for(int i = 0; i < l; i++) {
ans += bits[i] * p;
p <<= 1;
}
return ans;
}
1到n中二进制1的总数
统计从1到n的所有数字的二进制表示中的1的总数
- 1 <= n <= 1e9
int solve(int n) {
long long ans = 0;
int x = 31 - __builtin_clz(n);
for (int i = 0; i <= x; i++){
int c = 1 << i, cnt = 0;
int p = (n + 1) / c;
cnt = (p / 2) * c;
int d = (n + 1) % c;
if (p % 2 != 0) cnt += d;
ans = (ans + cnt) % 1000000007;
}
return ans;
}
询问mex数量
给一个0-n-1的排列P和Q个询问,每个询问给定 L1, L2, M1, M2 计算长度在[L1, L2]之间且 MEX值在[M1,M2] 之间的子数组数量。
- 1 <= n <= 1e6
- 1 <= q <= 2e5
- 1 <= L1 <= L2 <= N
- 0 <= M1 <= M2 <= N
分析
预处理函数 get(m, l) 长度大于等于l,且 MEX值大于等于m的子数组数量
void solve() {
int n, q;
cin >> n >> q;
vector<int> a(n), p(n), l(n + 1), r(n + 1);
for (int i = 0; i < n; ++i) {
cin >> a[i];
p[a[i]] = i + 1;
}
l[0] = 1e9, r[0] = -1;
for (int i = 1; i <= n; ++i) {
r[i] = max(r[i - 1], p[i - 1]);
l[i] = min(l[i - 1], p[i - 1]);
}
auto calc = [&](int m, int len) -> long long {
if (m > n || len <= 0) return 0;
if (m == 0) return 1ll * len * (2 * n - len + 1) / 2;
int y = n - r[m], x = l[m] - 1, k = r[m] - l[m] + 1;
if (k > len) return 0;
int left = len - k;
x = min(x, left), y = min(y, left);
int z = min(x, y) + 1;
long long res = z * (z + 1ll) / 2;
res += max(0ll, z * 1ll * (min(max(x, y), left) - z + 1));
z = max(x, y);
int num = min(x + y, left) - z;
z = min(x, y);
res += num * 1ll * (z - num + 1 + z) / 2;
return res;
};
auto get = [&](int l1, int l2, int m1, int m2) {
return calc(m1, l2) - calc(m1, l1 - 1) - calc(m2 + 1, l2) + calc(m2 + 1, l1 - 1);
};
for (int i = 0, l1, l2, m1, m2; i < q; ++i) {
cin >> l1 >> l2 >> m1 >> m2;
cout << get(l1, l2, m1, m2) << '\n';
}
}





