===
Index
二维矩阵中的好路径数
有一个n*m矩阵, 从(1,1)开始,走到(n,m),每一步只能向右走或向下走,如果经过路径上的数字之和能被k整除,则称为一条好的路径,求好路径的数目。
- 1 <= n, m <= 16
- 1 <= a[i], k <= 1e18
分析
双向dfs 类似题目cf 1006f
long long count_good_paths(vector<vector<long long>> &a, long long k) {
int n = a.size(), m = a[0].size();
long long res = 0;
map<long long, long long> mp[n];
function<void(int, int, long long)> dfs_pre = [&](int x, int y, long long s) {
if (x + y == (n + m - 2) / 2) {
mp[x][s]++;
return;
}
if (x + 1 < n) dfs_pre(x + 1, y, (s + a[x + 1][y]) % k);
if (y + 1 < m) dfs_pre(x, y + 1, (s + a[x][y + 1]) % k);
};
function<void(int, int, long long)> dfs_suf = [&](int x, int y, long long s) {
if (x + y == (n + m - 2) / 2) {
if (mp[x].count((((a[x][y] % k) - s + k) % k)))
res += mp[x][(((a[x][y] % k) - s + k) % k)];
return;
}
if (x > 0) dfs_suf(x - 1, y, (s + a[x - 1][y]) % k);
if (y > 0) dfs_suf(x, y - 1, (s + a[x][y - 1]) % k);
};
dfs_pre(0, 0, a[0][0] % k);
dfs_suf(n - 1, m - 1, a[n - 1][m - 1] % k);
return res;
}
最少操作次数
长度为n的整数数组a,每次操作可以选择任意元素将其加一。求最少的操作次数,使得: 任意长度大于等于3的子数组,其最大值都大于等于k.
- 1 <= n <= 1e5
- 0 <= a[i], k <= 1e9
示例: input: a = [2, 1, 1, 3], k = 5 output: 4 解释:4次操作可以将a变成[2,1,5,3]
void minOperations(vector<int> &a, int k) {
}
字典序最大子序列
给定长度为n的字符串s,对于i=1,…,n,求长度为i的字典序最大的子序列。例如 s="hrw"
ans = ["w", "rw", "hrw"]
- 1 <= n <= 1000
vector<string> maxLexsubSeq(string &s) {
int n = s.size();
vector<string> ans(n);
vector<pair<char,int>> a;
for (int i = 0; i < n; ++i) {
a.push_back({s[i], i});
}
sort(a.rbegin(), a.rend());
string t;
for (int i = 0; i < n; ++i) {
int j = i;
while (j > 0 && a[j].second < a[j - 1].second) {
swap(a[j], a[j - 1]);
j--;
}
t.insert(t.begin() + j, a[j].first);
ans[i] = t;
}
return ans;
}
好路径的数目
给定一棵n个节点的树,每个节点有一个值,一条好路径满足: 路径上任意节点的值出现的频率都至少是路径长度的一半(下取整)。节点u,v的路径长度定义为u,v简单路径上的节点数目。 求从节点1出发的好路径的数目。
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e5
int goodPaths(vector<vector<int>> &es, vector<int> &a) {
int n = a.size();
vector<vector<int>> g(n);
for (auto &e: es) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
int ans = 0;
map<int, int> mp;
function<void(int, int)> dfs = [&](int u, int fa) {
mp[a[u]]++;
if (mp.size() == 1) ans++;
else if (mp.size() == 2) {
int u = mp.begin()->second, v = mp.rbegin()->second;
if (abs(u - v) <= 1) ans++;
}
for (int v: g[u]) {
if (v == fa) continue;
dfs(v, u);
}
mp[a[u]]--;
if (mp[a[u]] == 0) mp.erase(a[u]);
};
dfs(0, -1);
return ans;
}
最少需要添加元素数
数组a,长度n,各元素互不相同,数组b,长度为m,元素可能有相同,求,至少在b中任意位置添加多少个数,使a变为b的子序列。
- 1 <= n,m <= 1e5
- 1 <= a[i], b[i] <= 1e9
输入格式: 第一行样例数t,每个样例第一行n,m, 后面两行分别为a,b
input:
1
5 6
1 2 3 4 5
2 5 6 4 9 12
output:
3
input:
2
9 19
1 2 4 6 15 18 19 24 29
12 19 19 5 26 2 23 9 23 14 29 7 28 24 28 29 21 16 16
16 10
1 2 3 4 8 9 11 12 14 17 19 21 24 26 28 29
11 18 8 9 9 15 24 26 16 18
output:
6
12
分析
求出a,b最长公共子序列k,答案为n-k,由于a中元素互不相同,最长公共子序列可以转化为最长上升子序列.
int lengthOfLIS(vector<int>& nums) {
vector<int> res;
for (int i = 0; i < nums.size(); ++i) {
auto it = lower_bound(res.begin(), res.end(), nums[i]);
if (it == res.end()) res.push_back(nums[i]);
else *it = nums[i];
}
return res.size();
}
int minAddElement(vector<int> &a, vector<int> &b) {
int n = a.size();
set<int> s(a.begin(), a.end());
vector<int> c;
for(auto &x: b) if (s.count(x))
c.push_back(x);
int k = lengthOfLIS(c);
return n - k;
}
最多出现次数
长度为n的数组a,每次可以选择任意下标,将该下标处得到元素加k,但是其余元素会减k,可以进行任意次操作,你的目标是使数组中不同的元素个数最少,求最后数组中出现次数最多的元素出现了多少次
- 1 <= n <= 1000
- 0 <= k, a[i] <= 1000
分析
每次操作相当于选择一个元素,将其加2k, 当两个元素模 2k的余数相同时,两个元素能变成相同元素。
示例1 input
3 1
3 1 3
output:
3
示例2 input
3 1
1 2 2
output:
2
int maxtimes(vector<int> &a, int k) {
int m = 2 * k, n = a.size();
map<int, int> mp;
for (int i = 0; i < n; ++i) {
int x = m > 0 ? a[i] % m : a[i];
mp[x]++;
}
int ans = 0;
for (auto &[_, v]: mp) {
ans = max(ans, v);
}
return ans;
}
树上路径的位运算
n个节点的树,每条边有个权重,用数组w给出,q个询问,每个询问给定x,y,对于每个询问,计算x,y简单路径上权重的 xor, and, or值。
- 1 <= n <= 1e5
- 0 <= w[i] <= 1e9

vector<vector<int>> bitwise_tree(vector<vector<int>> &es, vector<vector<int>> &q) {
int n = es.size() + 1;
vector<vector<pair<int,int>>> g(n);
LCA lca(n);
for (auto& e: es) {
g[e[0]].push_back({e[1], e[2]});
g[e[1]].push_back({e[0], e[2]});
lca.add_edge(e[0], e[1]);
}
lca.build();
vector s(n, vector<int>(32));
vector<int> e(n);
function<void(int, int)> dfs = [&](int u, int fa) {
for (auto &[v, p] : g[u]) {
if (v != fa) {
for (int i = 0; i < 32; ++i)
s[v][i] = s[u][i] + ((p & (1 << i)) ? 1 : 0);
e[v] = e[u] + 1;
dfs(v, u);
}
}
};
dfs(0, -1);
vector<vector<int>> ans(q.size());
for (int i = 0; i < q.size(); ++i) {
int x = q[i][0], y = q[i][1], u = lca.get_lca(x, y);
int _xor = 0, _and = 0, _or = 0, cnt = e[x] + e[y] - 2 * e[u];
for (int i = 0; i < 32; ++i) {
int c = s[x][i] + s[y][i] - 2 * s[u][i];
if (c % 2 == 1) _xor |= (1 << i);
if (c >= 1) _or |= (1 << i);
if (c == cnt) _and |= (1 << i);
}
ans[i] = {_xor, _and, _or};
}
return ans;
}
将数组变为0的最小的k
给定长度为n的数组a和整数m,使用如下条件将数组元素全部变为0: 选择一个整数k,执行下面操作至多m次
- 选择一个下标i (0 <= i < n)
- 赋值 a[i] = max(0, a[i] - k)
求满足上述条件的最小的k。
- 1 <= n <= 1e5
- n <= m <= 1e12
- 1 <= a[i] <= 1e12
long long minKzeroArray(vector<long long> &a, int m) {
long long l = 0, r = 1e12, mn = r;
while (l <= r) {
long long md = (l + r) / 2;
long long c = 0;
for (auto &x: a)
c += max(0ll, (x + md - 1) / md);
if (c <= m) {
mn = md;
r = md - 1;
} else l = md + 1;
}
return mn;
}
最多赢的分数
有偶数个数值,两位玩家A和B,从数组两端取数,A先手,B后手,B始终采取贪心策略,每次取两端中更大的一个,求A采取最有策略的条件下,最红与B得分的最大差值(得分为每个人所选数的和)
- 1 <= n <= 1000
- n是偶数
- sum(a[1,..n]) <= 1e6
int maxScodeDiff(vector<int> &a) {
int n = a.size();
function<pair<int,int>(int, int)> dfs1;
function<pair<int,int>(int, int)> dfs2;
map<pair<int,int>,pair<int,int>> dp1,dp2;
dfs1 = [&](int i, int j) {
if (dp1.count({i, j})) return dp1[{i, j}];
if (i == j) {
dp1[{i, j}] = {a[i], 0};
return dp1[{i, j}];
}
pair<int, int> d1{a[i] + dfs2(i + 1, j).first, dfs2(i + 1, j).second};
pair<int, int> d2{a[j] + dfs2(i, j - 1).first, dfs2(i, j - 1).second};
if (d1.first - d1.second >= d2.first - d2.second) {
dp1[{i, j}] = d1;
return d1;
}
dp1[{i, j}] = d2;
return d2;
};
dfs2 = [&](int i, int j) {
if (dp2.count({i, j})) return dp2[{i, j}];
if (i == j) {
dp2[{i, j}] = {0, a[i]};
return dp2[{i, j}];
}
pair<int, int> d1{dfs1(i + 1, j).first, dfs1(i + 1, j).second + a[i]};
pair<int, int> d2{dfs1(i, j - 1).first, dfs1(i, j - 1).second + a[j]};
if (a[i] > a[j] || (a[i] == a[j] && d1.first - d1.second >= d2.first - d2.second)) {
dp2[{i, j}] = d1;
return d1;
}
dp2[{i, j}] = d2;
return d2;
};
auto [x, y] = dfs1(0, n - 1);
return x - y;
}
异或三元组之和
长度为n的数组a,q次询问,每次询问给定[l,r],对于每个询问,求所有满足l<=i<j<k<=r,的三元组异或和之和,sum(a[i]^a[j]^a[k])
- 1 <= n, q <= 1e5
- 1 <= a[i] <= 1e12
- 1 <= l <= r <= n
vector<int> xor_sum_triples(vector<long long> &a, vector<vector<int>> &qs){
int n=sz(a),m=sz(qs);
const int K=40,mod=1e9+7; //根据数据范围调整
vector<long long> po(K,1);
for(int i=1;i<K;++i)
po[i]=(po[i-1]*2)%mod;
vector<array<int,K>>pre(n+1);
f0(n){
f2(j,K){
pre[i+1][j]=pre[i][j];
if((a[i]>>j)&1)pre[i+1][j]++;
}
}
vector<int> c(m);
f0(m){
ll s=0;
int len=qs[i][1]+1-qs[i][0];
f2(j,K){
int c1=pre[qs[i][1]+1][j]-pre[qs[i][0]][j],c0=len-c1;
ll p=(c1*1ll*c0*(c0-1)/2)%mod;
p=(p+(c1*1ll*(c1-1)*(c1-2))/6)%mod;
p=(p*po[j])%mod;
s=(s+p)%mod;
}
c[i]=s;
}
return c;
}
部署服务的最小代价
n个服务器,两个数组a,b。a[i]表示将第i个服务器用作类型1的代价,b[i]表示将第i个服务器用作类型2的代价. 每个服务器可以作为类型1,或者作为类型2(当相邻元素i-1,或i+1中存在类型1时),且类型2必须至少连续两个相邻服务器一起设定。 求满足条件的所有服务器的最小代价。
- 1 <= n <= 1e6
- 1 <= a[i],b[i] <= 1e9
eg1:
input:
10
1 2 1 3 4 2 1 2 3 1
5 5 1 1 1 5 5 1 1 1
output
12
eg2
input:
5
3 5 2 1 9
1 1 10 5 3
output
12
long long min_cost_server(vector<int> &a, vector<int> &b){
int n=a.size();
const ll inf=1e18;
vector<vector<ll>> f(n+1,vector<long long>(3));
f[1][0]=a[0], f[1][1]=b[0], f[1][2]=inf;
for(int i=1;i<n;++i){
f[i+1][0]=a[i]+min(f[i][0],f[i][2]);
f[i+1][1]=b[i]+min(f[i][0],f[i][1]);
f[i+1][2]=b[i]+b[i-1]+min(f[i-1][0],f[i-1][1]);
}
return min(f[n][0],f[n][2]);
}
数组最小值的最大值与最小代价
3个长度为n的整数数组A,B,C,对于每个i,A[i]>=B[i]成立,可以在A上作如下操作任意次: 选择两个下标i,j满足A[j]>B[j], 使A[i]+=1,A[j]-=1,操作代价是C[j]. 求任意次操作后,数组A中最小值的最大可能值,以及到达该值所需的最小代价,模1e9+7.
- 1 <= n <= 1e5
- 1 <= a[i],b[i],c[i] <= 1e9
const int mod=1e9+7;
vector<int> query_and_pair(vector<int> &a, vector<int> &b, vector<int> &c) {
int n=a.size();
int l=Mn(a),r=Sm(a)/n,x=l;
ll s=0,y=0;
auto chk=[&](int x){
s=0;
f0(n){
if(a[i]<x){
s-=x-a[i];
}else{
s+=a[i]-max(b[i],x);
}
}
return s>=0;
};
while(l<=r){
int md=(l+r)/2;
if(chk(md)){
x=md;
l=md+1;
}else r=md-1;
}
vector<int> v(n);
iota(all(v),0);
sort(all(v),[&](int i, int j){return c[i]<c[j];});
s=0;
f0(n)if(a[i]<x)s+=x-a[i];
f0(n){
if(a[v[i]]>x){
int t=a[v[i]]-max(b[v[i]],x);
cmn(t,s);
s-=t;
y=(y+t*1ll*c[v[i]])%mod;
if(s==0)break;
}
}
return {x,(int)y};
}
最小初始值
给定两个长为n的数组a,b, 可以按任意顺序遍历数组,求最小的x,满足按照某种遍历顺序,遍历到每一个下标i时,都有 x>=a[i], 遍历下标i后,执行 x-=b[i]操作。
- 1 <= n <= 1e5
- 1 <= b[i] <= a[i] <= 1e5
分析
二分+贪心
long long minInitValue(vector<int> &a, vector<int> &b) {
int n=sz(a);
vector<int> p(n);
iota(all(p),0);
sort(all(p),[&](int i, int j){
return a[i]-b[i]>a[j]-b[j];
});
auto c=b_search<ll>(Mx(a),Sm(a),1,[&](ll x){
f0(n){
if(x>=a[p[i]]){
x-=b[p[i]];
}else return 0;
}
return 1;
});
return c;
}
amazon
找出数组第k大和
给你一个整数数组 nums 和一个正整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。
数组的 第 k 大和 定义为:可以获得的第k个最大子序列和(子序列和允许出现重复)
返回数组的 第 k 大和 。
注意:空子序列的和视作 0
- 1 <= nums.size() <= 1e5
- -1e9 <= nums[i] <= 1e9
- 1 <= k <= min(2000, 2^n)
分析
简化问题
考虑本题的简化问题:给定 n 个非负数 a[1],…,a[n],求第 k 个最 小 的子序列和。
这是一个经典问题。我们先把所有数从小到大排序,记(s,i) 表示一个总和为 s, 且最后一个元素是第 i个元素的子序列。
我们用一个小根堆维护(s,i), 一开始堆中只有一个元素(a[1],1), 当我们取出堆顶元素(s,i)时,可以进行以下操作
- 把a[i+1]接到这个子序列的后面形成新的子序列,也就是将(s+a[i+1],i+1)放入堆中
- 把子序列中的a[i],直接替换为a[i+1],也就是将(s+a[i+1]-a[i],i+1)放入堆中
第 (k−1) 次取出的 (s,i) 中的 s 就是答案(k=1 时答案为空集之和,也就是 0)。
这个做法的正确性基于以下事实:
- 这种方法能不重不漏地生成所有子序列。
- 每次放进去的数不小于拿出来的数
最小和变最大和
实际上,求第 k 个最大的子序列和,与求第 k 的最小的子序列和是一样的。我们求出 k 小子序列后取反(选择不在答案中的所有元素作为新的答案),就能得到 k 大子序列。因此所有元素之和减去 k 小子序列和,就能得到 k 大子序列和。
引入负数
回到原问题,考虑给定的数中有负数的情况, 首先计算 m 表示所有负数的和,然后把所有负数变成它们的绝对值(这样就回到了全是非负数的情况)。答案就是 m 加上 k 大子序列和。
为什么这样是对的?考虑由此得到的 k 大子序列,它实际上唯一对应了一个原有的子序列。我们举个例子:
- 一开始a = [-3, -2, -1, 4, 5, 6]
- 经过转换之后,我们得到k大子序列{2,1,5,6}
- 对于所有在该子序列中的非负数,令它成为答案的一部分,也就是说 5 和 6 是答案的一部分;
- 对于所有不在该子序列中的负数,令它成为答案的一部分,也就是说 −3 是答案的一部分;
- 最后得到真实答案 [-3,5,6]
typedef pair<long long, int> pli;
long long kMaxsum(vector<int> &a, int k) {
int n = a.size();
long long s = 0, sn = 0;
for (int &x : a) {
s += x;
if (x < 0) sn += x, x = -x;
}
sort(a.begin(), a.end());
long long ans = 0;
priority_queue<pli, vector<pli>, greater<pli>> pq;
pq.push({a[0], 0});
for (int i = 2; i <= k; ++i) {
auto [x, y] = pq.top(); pq.pop();
ans = x;
if (y == n - 1) continue;
pq.push({x + a[y + 1], y + 1});
pq.push({x + a[y + 1] - a[y], y + 1});
}
return s - (sn + ans);
}
按从大到小返回前k大和
typedef pair<long long, int> pli;
vector<long long> kMaxsum(vector<int> &a, int k) {
int n = a.size();
long long s = 0, sn = 0;
for (int &x : a) {
s += x;
if (x < 0) sn += x, x = -x;
}
sort(a.begin(), a.end());
vector<long long> ans{s - sn};
priority_queue<pli, vector<pli>, greater<pli>> pq;
pq.push({a[0], 0});
for (int i = 2; i <= k; ++i) {
auto [x, y] = pq.top(); pq.pop();
ans.push_back(s - sn - x);
if (y == n - 1) continue;
pq.push({x + a[y + 1], y + 1});
pq.push({x + a[y + 1] - a[y], y + 1});
}
return ans;
}
最大递增物品和
给定一个长度为n的数组,a[i]表示第i堆有a[i]个物品,你可以选择一个连续区间进行取货,取出的物品数量必须是递增的,求能取出的最大物品。 示例:a=[7,4,5,2,6,5] 你可以选择[7,4,5]这个区间,能取到的最多物品为[3,4,5],其和为12,因为取出的物品必须是递增的,你也可以选择[5,2,6,5]这个区间,分别能取出[1,2,4,5],总和也是12.
- 1 <= n <= 1e5
分析
dp[i] 表示以 i 位置元素结尾的最大物品数,则 dp[i] = 等差数列求和[j..i] + dp[j]。 利用单调栈寻找 j 的位置,即 last smaller element,条件为横坐标的差值。
long long maxIncresceSum(vector<int> &a) {
int n = a.size(), k;
long long s = 0;
vector<long long> dp(n);
stack<int> sk;
for (int i = 0; i < n; ++i) {
while (!sk.empty() && a[sk.top()] >= a[i] - (i - sk.top())) sk.pop();
k = sk.empty() ? min(i + 1, a[i]) : i - sk.top();
dp[i] = (a[i] + a[i] - len + 1) * len / 2 + (sk.empty() ? 0 : dp[sk.top()]);
s = max(s, dp[i]);
sk.push(i);
}
return s;
}
统计子串数目
给定长度为n的二进制字符串,统计有多少个子串满足下述条件:
- ‘0’ 和 ‘1’ 都是连续出现的
- ‘0’ 的数目 等于 ‘1’ 的数目
- 1 <= n <= 5e5
long long countSumString(string &s) {
long long ans = 0, x = 0, y = 1;
for (int i = 1; i < (int)s.size(); ++i) {
if (s[i] != s[i - 1]) {
ans += min(x, y);
x = y;
y = 1;
}else y++;
}
ans += min(x, y);
return ans;
}
字典序最小的字符串
给你一个字符串 s 和一个机器人,机器人当前有一个空字符串 t 。执行以下操作之一,直到 s 和 t 都变成空字符串:
- 删除字符串 s 的 第一个 字符,并将该字符给机器人。机器人把这个字符添加到 t 的尾部。
-
删除字符串 t 的 最后一个 字符,并将该字符给机器人。机器人将该字符写到纸上。 请你返回纸上能写出的字典序最小的字符串。
- 1 <= s.size() <= 1e5
- s只包含小写字母
分析
本题是经典贪心:求出栈序列的最小字典序。 我们首先将题目描述进行转化:有一个初始为空的栈,给定字符的入栈顺序,求字典序最小的出栈序列。
当一个字符入栈后,我们持续检查栈顶元素 c。设还未入栈的字符中,字典序最小的字符是 m,有以下两种情况。
- c≤m:此时弹出 c 最优。如果此时按兵不动,下一个出栈的将会是大等于 c 的字符,答案不会变优。
- c>m:此时不弹出 c,等待后续更小的字符入栈。
所有字符都入栈后,栈内的剩余字符按顺序弹出即可。复杂度 \mathcal{O}(n)O(n)。
string robotWithString(string s) {
int n = s.size();
vector<char> f(n + 1);
f[n] = 'z' + 1;
for (int i = n - 1; i >= 0; i--) f[i] = min(f[i + 1], s[i]);
string ans;
stack<char> stk;
for (int i = 0; i < n; i++) {
stk.push(s[i]);
while (!stk.empty() && stk.top() <= f[i + 1]) ans.push_back(stk.top()), stk.pop();
}
return ans;
}
子串得分
字符串s,长度为n,只包含小写字母,字符串得分定义为字符串中各字符出现次数的异或和。有两种不同query.
- 1 L R: 求s[L..R]的score
-
2 X Y: 将s[x] 赋值为第i个字符
- 1 <= n <= 1e5
- 1 <= q <= 1e5
- 1 <= x,l,r <= n
- 1 <= y <= 26
vector<int> stringScore(string &s, vector<vector<int>> &qs){
int n = s.size();
vector tr(n, vector<int>(26));
auto add = [&](int x, int y, int c) {
for (; x <= (int)tr.size(); x += x & -x) tr[x - 1][y] += c;
};
auto ask = [&](int x, int y) {
int res = 0;
for (; x > 0; x -= x & -x) res += tr[x - 1][y];
return res;
};
for (int i = 0; i < n; ++i) {
add(i + 1, s[i] - 'a', 1);
}
vector<int> ans;
for(auto& q: qs) {
int op = q[0], x = q[1], y = q[2];
if (op == 1) {
int res = 0;
for (int i = 0; i < 26; ++i) {
int cnt = ask(y + 1, i) - ask(x, i);
res ^= cnt;
}
ans.push_back(res);
} else {
int c = s[x] - 'a';
add(x + 1, c, -1);
add(x + 1, y, 1);
s[x] = char('a' + y);
}
}
return ans;
}
好字符串
给定字符串s(只包含小写字母),长度为n,q个区间[l,r],和一个1-N的排列。
每一次操作,你会按照排列中的元素下标顺序删掉字符串中的元素,但剩余元素位置不变。 例如 s = “acbca”, 排列 = [3,4,1,5,2] 第1次操作,s变为 ac_ca 第2次操作,s变为 ac__a 第3次操作,s变为 c__a 第4次操作,s变为 _c__ 第5次操作,s变为 _____
求至少操作多少次,使得每个区间构成的子串中的元素都是不同的(没有重复元素)
- 1 <= n <= 1e5
- 1 <= q <= 1e5
- 1 <= a[i] <= n
- 1 <= l <= r <= n
input1:
1
8 3
abbabaab
6 3 5 1 4 2 7 8
1 3
4 7
3 5
output1:
5
input2:
1
5 2
aaaaa
2 4 1 3 5
1 2
4 5
output2:
2
int minOperations(string &s, vector<vector<int>> &qs, vector<int> a) {
int n = s.size();
int l = 0, r = n, mn = n;
auto chk = [&](int x) {
string t = s;
for (int i = 0; i < x; ++i) {
t[a[i]] = '_';
}
vector<vector<int>> p(n+1,vector<int>(26));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < 26; ++j) {
p[i + 1][j] = p[i][j] + (t[i] == 'a' + j);
}
}
for (auto &q : qs) {
for (int i = 0; i < 26; ++i)
if (p[q[1] + 1][i] - p[q[0]][i] > 1) return 0;
}
return 1;
};
while (l <= r) {
int md = (l + r) / 2;
if (chk(md)) {
mn = md;
r = md - 1;
}else l = md + 1;
}
return mn;
}
数组严格递增的最少操作次数
一个长度为n的数组,每次操作可以选择数组中任意一个数+1,或者-1, 求让数组变为严格递增数组所需的最少操作次数。 可以让数组中元素变为0或负数。
- 1 <= n <= 3000
- 1 <= a[i] <= 1e9
分析
问题1 :给定数组,最少操作次数(+1,-1)使数组中元素全部相等。
对于每一个前缀数组,其最优方案为让所有元素变为该数组的中位数,可以使用两个堆维护数据流中的中位数。
问题2: 给定数组,最少操作次数(+1,-1) 使数组中元素变为不下降序列。
首先所有数最后所变成的数一定是原序列中有的数,设a为原数组,b为a排序后的数组,且b中无重复元素。
f[i][j] 表示让数组中前i个元素非递减,且第i个元素最大为b[j]的情况下的最少操作次数,最终答案为f[n][k], k为b数组的长度。
f[1][1] = abs(a[1] - b[1])
f[1][j] = min(f[1][j - 1], abs(a[1] - b[j]))
f[i][1] = abs(a[i] - b[1]) + f[i - 1][1]
f[i][j] = min(f[i][j - 1], f[i - 1][j] + abs(a[i] - b[j]))
本问题:
dp[i]:使前i个元素递增的最少操作次数, 首先操作a[i]=a[i]-i,则该问题转化为问题2.
long long minOperations(vector<int> &a) {
int n = a.size();
vector<long long> b(n), f(n);
for (int i = 0; i < n; ++i) {
a[i] -= i;
b[i] = a[i];
}
sort(b.begin(), b.end());
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
f[j] += abs(a[i] - b[j]);
if (j > 0 && f[j - 1] < f[j]) f[j] = f[j - 1];
}
}
return f[n - 1];
}
方法2
- 时间复杂度
O(n*log(n))
long long minOperations(vector<int> &a) {
int n = a.size();
long long ans = 0;
priority_queue<int> q;
for (int i = 0; i < n; ++i) {
a[i] -= i;
q.push(a[i]);
if (q.top() > a[i]) {
ans += q.top() - a[i];
q.pop();
q.push(a[i]);
}
}
return ans;
}
n次操作后的最大得分
长度为2n的数组,需要执行n次操作,第i次操作中(i=1,..n):
- 选择两个数组中的元素x,y,本次操作得分为 i * gcd(x,y),
- 从数组中删除x,y
求n次操作后的最大得分。
- 1 <= n <= 7
- 1 <= a[i] <= 1e6
分析
状态压缩dp。
int maxSocre(vector<int> &a) {
int n = a.size();
vector g(n, vector<int>(n));
for (int i = 0; i < n; ++i)
for (int j = i + 1; j < n; ++j)
g[i][j] = gcd(a[i], a[j]);
vector dp(n + 1,vector<int> (1 << n));
function<int(int, int)> dfs =[&](int idx, int st) {
if (idx - 1 == n / 2) return 0;
if (dp[idx][st]) return dp[idx][st];
int res = 0;
for (int i = 0; i < n; ++i) {
if ((st >> i) & 1) continue;
for (int j = i + 1; j < n; ++j) {
if ((st >> j) & 1) continue;
res = max(res, idx * g[i][j] + dfs(idx + 1, st | (1 << i) | (1 << j)));
}
}
return dp[idx][st] = res;
};
return dfs(1, 0);
}
包含k个zero子序列的最短字符串长度
输入k,求包含大于等于k个”zero”子序列的最短字符串长度。例如, k = 2时,”zzero”, “zeero”,”zerro”,”zeroo” 都包含2个zero子序列,且长度最短,因此答案是5.
- 1 <= k <= 1e9
类似题目:cf1368b
// s = "zero" 或者其他字符串
int minimumLengStr(string &s, int k) {
int n = s.size();
vector<long long> a(n, 1);
long long sum = 1;
for (int i = 0; sum < k; i = (i + 1) % n) {
sum = sum / a[i] * (a[i] + 1);
++a[i];
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += a[i];
}
return ans;
}
如果需要输出其中满足条件的一个最短字符串,则
for (int i = 0; i < n; ++i) {
for (int j = 0; j < a[i]; ++j)
cout << s[i];
}
pair数目
给q个pair (l,r),所有l互不相同,和长度为n的数组a,求有多少个pair对(i,j)满足i<j,且a[i],a[j]和q个pair中的恰好一个相等。
- 1 <= n, q <= 1e5
- 1 <= l, r, a[i] <= 1e9
// Discrete
// FenwickTree
long long pair_of_pairs(vector<vector<int>> &qs, vector<int> &a) {
map<int,vector<int> >mp;
vector<int> b;
for(auto&e:qs){
mp[e[0]].push_back(e[1]);
b.push_back(e[1]);
}
each(x,a)b.push_back(x);
Discrete<int> v(b);
int m=v.size(),n=sz(a);
FenwickTree<int> f(m);
each(x,a) f.add(v(x),1);
ll c=0;
f0(n){
f.add(v(a[i]),-1);
if(!mp.count(a[i])) continue;
for(auto&x:mp[a[i]]){
c+=f.get(v(x));
}
}
return c;
}
所有子数组的不同元素数量的总和
给定长度为n的数组a,对a的所有子数组包含不同元素的数量求和。
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e9
long long distinct_sum(vector<int> &a) {
int n=a.size();
unordered_map<int, int> mp;
long long c=0;
for (int i = 0; i < n; ++i) {
int l = mp.count(a[i])?mp[a[i]]:-1;
c+=(i-l)*1ll*(n-i);
mp[a[i]]=i;
}
return c;
}
所有子数组的不同元素数量的中位数
给定长度为n的数组a,将a的所有子数组包含不同元素的数量组成一个新数组b,求b的中位数。 例如: a = [1,2,2],则 b=[1,1,1,2,1,2]。 中位数: [1,5,8]中位数是5,[2,3,7,8]中位数是3.
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e9
int subarr_unque_median(vector<int> &a) {
int n=sz(a);
ll t=n*1ll*(n+1)/2;
t=(t+1)/2;
auto c=b_search<int>(0,n,0,[&](int x){
unordered_map<int, int> mp;
ll s=0;
for(int i=0,j=0;i<n;++i){
mp[a[i]]++;
while(j<=i&&sz(mp)>x){
mp[a[j]]--;
if(mp[a[j]]==0)mp.erase(a[j]);
j++;
}
s+=i-j+1;
}
return s<t;
});
return c+1;
}
非递减数组最大长度
长度为n的数组,每次操作可以从数组中选择一个子数组,将子数组替换为子数组元素和,可以操作任意次,求能获得的非递减子数组最大长度。
- 3 <= n <= 1e5
- 1 <= a[i] <= 1e5
int findMaximumLength(vector<int> &nums) {
int n = nums.size();
vector<long long> s(n + 1), last(n + 1);
vector<int> f(n + 1), q(n + 1);
int front = 0, rear = 0;
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + nums[i - 1];
while (front < rear && s[q[front + 1]] + last[q[front + 1]] <= s[i]) {
front++;
}
f[i] = f[q[front]] + 1;
last[i] = s[i] - s[q[front]];
while (rear >= front && s[q[rear]] + last[q[rear]] >= s[i] + last[i]) {
rear--;
}
q[++rear] = i;
}
return f[n];
}
最大最小生成树
n个节点,每个节点有一个值a[i], 连接节点i 和节点j 边的代价为 abs(a[i] - a[j]),求使n个节点连通的最大代价和最小代价
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e9
分析
n个点两两组和,共有 n*(n-1)/2条连边方法,本质是求,差值最小的n-1个pair的差值之和和差值最大的n-1个pair的差值之和。
先二分出对应差值,再双指针求和,时间复杂度 O(n*log(n))
vector<long long> cost_tree(vector<int> &a) {
int n = a.size();
if (n == 1) return {0ll, 0ll};
sort(a.begin(), a.end());
int mn = a[1] - a[0], mx = a[n - 1] - a[0];
for (int i = 2; i < n; ++i) {
mn = min(mn, a[i] - a[i - 1]);
}
auto get_kth_diff = [&](long long k) {
int l = mn, r = mx, res = mx;
while (l <= r) {
int md = (l + r) / 2;
long long s = 0;
for (int i = 0, j = 0; i < n; ++i) {
while (j + 1 < n && a[j + 1] - a[i] <= md) j++;
s += j - i;
if (s >= k) break;
}
if (s >= k) {
res = md;
r = md - 1;
} else l = md + 1;
}
return res;
};
long long s1 = 0, s2 = 0;
int t1 = get_kth_diff(n - 1), t2 = get_kth_diff(n * 1ll * (n - 1) / 2 - n + 2);
int cnt1 = 0, cnt2 = 0;
vector<long long> pre(n + 1);
for (int i = 0; i < n; ++i) {
pre[i + 1] = pre[i] + a[i];
}
for (int i = 0, j = 0; i < n; ++i) {
while (j + 1 < n && a[j + 1] - a[i] < t1) {
j++;
}
int x = j - i;
cnt1 += x;
s1 += pre[j + 1] - pre[i + 1] - x * 1ll * a[i];
}
s1 += (n - 1 - cnt1) * 1ll * t1;
for (int i = 0, j = 0; i < n; ++i) {
while (j < n && a[j] - a[i] <= t2) j++;
if (j == n) break;
int x = n - j;
cnt2 += x;
s2 += pre[n] - pre[j] - x * 1ll * a[i];
}
s2 += (n - 1 - cnt2) * 1ll * t2;
return {s1, s2};
}
所有pair连接和
给定长度为n的数组,f(x, y)表示将x和y连接形成的数,例如 f(34,212) = 34212, 求 f(a[0],a[1])+…+f(a[0],a[n-1])+…+f(a[n-2],a[n-1])
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e9
int pair_sum(vector<int> &a) {
int n = a.size();
map<int, int> mp;
vector<int> p(n);
for (int i = 0; i < n; ++i) {
string s = to_string(a[i]);
p[i] = s.size();
mp[p[i]]++;
}
mint c = 0;
for (int i = 0; i < n; ++i) {
mp[p[i]]--;
for (auto &[k, v] : mp) {
mint d = a[i];
d *= mint(10).pow(k);
d *= v;
c += d;
}
c += mint(i) * a[i];
}
return c.val();
}
microsoftoa
统计非重叠区间数
n个区间,每个区间表示为[l,r],从中选择3个互不重叠的区间,共有多少种方案。注意 [2,3],[3,5]算有重叠元素3.
- 1 <= n <= 1e5
- 1 <= l <= r <= 1e9
分析
统计每个区间,开始位置左边有多少个不重叠区间,结束位置右边有多少个满足条件的区间即可。
long long countRanges(vector<vector<int>> &rs) {
long long ans = 0, cnt_l = 0, n = rs.size();
priority_queue<int, vector<int>, greater<int>> q;
sort(rs.begin(), rs.end(),[&](auto &x, auto &y){
return x[0] < y[0];
});
for (int i = 0; i < n; ++i) {
while (q.size() && q.top() < rs[i][0]) {
cnt_l++; q.pop();
}
int l = i + 1, r = n - 1, cnt_r = 0;
while (l <= r) {
int md = (l + r) / 2;
if (rs[md][0] > rs[i][1]) {
cnt_r = n - md;
r = md - 1;
}else l = md + 1;
}
ans += cnt_l * cnt_r;
q.push(rs[i][1]);
}
return ans;
}
打开所有灯泡的最小代价
n个灯泡排成一排,其中有一些打开,有一些是关闭的,现在需要将关闭的灯泡用电线直接或间接连接到已打开的灯泡,给定每个灯泡到第一个灯泡到距离,求最短需要多少电线。
// DSU
int minLength(vector<int> &blubs, vector<int> &d) {
int n = blubs.size(), cnt1 = 0;
DSU p(n + 1);
vector<vector<int>> es;
for (int i = 0; i < n; ++i) {
if (blubs[i] == 1) {
p.merge(i, n);
cnt1++;
} else {
if (i > 0) es.push_back({i, i - 1, d[i] - d[i - 1]});
if (i < n - 1) es.push_back({i, i + 1, d[i + 1] - d[i]});
}
}
if (cnt1 == 0) return -1;
int ans = 0;
sort(es.begin(), es.end(),[&](auto &x, auto &y){
return x[2] < y[2];
});
for(auto &e : es) {
int x = e[0], y = e[1], c = e[2];
if (!p.same(x, y)) {
ans += c;
p.merge(x, y);
}
}
return ans;
}
前缀和非负的最少移动次数
长度为n的数组,每次操作可以选择一个负数移到末尾,求使数组所有前缀和都非负的最少操作次数。
- 1 <= n <= 1e5
- -1e9 <= a[i] <= 1e9
- sum(a[1..n]) >= 0
int minSwaps(vector<int> &a) {
priority_queue<int, vector<int>, greater<int>> q;
long long s = 0;
int ans = 0;
for (auto & x : a) {
s += x;
if (x < 0) q.push(x);
if (s < 0) {
s -= q.top();
q.pop();
ans ++;
}
}
return ans;
}
能否从b运到e
有n个吊机,位置用数组p给出,每个吊机手臂长度用数组a给出,第i个吊机可以将[p[i]-a[i], p[i]+a[i]] 区间内的任意物体移到区间内任意位置,给你两个位置b和e,能否从b运到e.
- 1 <= n <= 1e5
- 0 <= b, e, p[i] <= 1e9
- 1 <= a[i] <= 1e9
分析
构造n个区间,合并有交集区间,判断b,e是否在同一个区间内即可。
bool canMove(vector<int> &a, vector<int> &p, int b, int e) {
int n = a.size();
vector<array<int, 2>> ranges(n), tmp;
for (int i = 0; i < n; ++i) {
ranges[i] = {p[i] - a[i], p[i] + a[i]};
}
sort(ranges.begin(), ranges.end(), [&](auto &x, auto &y){
if (x[0] != y[0]) return x[0] < y[0];
return x[1] < y[1];
});
tmp.push_back(ranges[0]);
for (int i = 1; i < n; ++i) {
if (ranges[i][0] <= tmp.back()[1])
tmp.back()[1] = max(tmp.back()[1], ranges[i][1]);
else
tmp.push_back(ranges[i]);
}
auto get = [&](int x) {
int l = 0, r = tmp.size() - 1, c = -1;
if (x < tmp[0][0] || x > tmp[r][1]) return -1;
while (l <= r) {
int md = (l + r) / 2;
if (x >= tmp[md][0] && x <= tmp[md][1]) {
c = md;
break;
} else if (x < tmp[md][0]) r = md - 1;
else l = md + 1;
}
return c;
};
int x = get(b), y = get(e);
return (x != -1 && y != -1 && x == y);
}
相等数组的最长长度
输入两个数组a,b, 每次操作可以选择一个数组,将其任意的一个子数组替换为一个整数,该整数位子数组元素之和。 可以操作任意次,求将a,b变为两个相等数组,能获得的最长数组长度,如果无法变为相等,返回-1.
- 1 <= n, m <= 1e5
- 1 <= a[i], b[i] <= 1e4
类似题目 cf 1036d
int maxLengEqual(vector<long long> &a, vector<long long> &b) {
int n = a.size(), m = b.size();
long long s1 = accumulate(a.begin(), a.end(), 0ll);
long long s2 = accumulate(b.begin(), b.end(), 0ll);
if (s1 != s2) return -1;
int ans = 0;
for (int i = 0, j = 0; i < n && j < m;) {
if (a[i] == b[j]) {
ans++, i++, j++;
} else if(a[i] > b[j]) {
if (j + 1 < m) b[j + 1] += b[j];
j++;
} else {
if (i + 1 < n) a[i + 1] += a[i];
i++;
}
}
return ans;
}
最大收益座位安排
影院有n个座位,第i个座位价值a[i], 有m个团队,第i个团队有b[i]人,每个团队的座位要坐到一块,任意给m个团队安排座位,求能获得的最大收益。
- 1 <= n <= 500
- 1 <= m <= 13
- 1 <= a[i] <= 1e9
- 1 <= b[i] <= n
- b[1] + b[2] + .. + b[m] <= n
示例输入:
6 2
1 7 8 2 3 9
2 1
输出
24
状态压缩dp
long long maxProfit(vector<int> &a, vector<int> &b) {
int n = a.size(), m = b.size();
vector<long long> p(n + 1);
for (int i = 0; i < n; ++i) {
p[i + 1] = p[i] + a[i];
}
vector dp(n + 1, vector<long long>((1 << m), -1));
long long inf = 1e18, ans = 0;
function<long long(int, int)> dfs = [&](int i, int mask) {
if (i >= n) return 0;
if (dp[i][mask] >= 0) return dp[i][mask];
dp[i][mask] = 0;
for (int k = 0; k < m; ++k) {
if (!(mask & (1 << k))) {
dp[i][mask] = max(dp[i][mask], p[i + b[k]] - p[i] + dfs(i + b[k], mask | (1 << k)));
}
}
return dp[i][mask] = max(dp[i][mask], dfs(i + 1, mask));
};
return dfs(0, 0);;
}
code2 ,未验证
long long maxProfit1(vector<int> &a, vector<int> &b) {
int n = a.size(), m = b.size();
vector<long long> p(n + 1);
for (int i = 0; i < n; ++i) {
p[i + 1] = p[i] + a[i];
}
vector dp(n + 1, vector<long long>((1 << m), -1));
long long inf = 1e18, ans = 0;
function<long long(int, int)> dfs = [&](int i, int mask) -> long long {
if (i >= n) return 0;
if (dp[i][mask] >= 0) return dp[i][mask];
dp[i][mask] = 0;
for (int k = 0; k < m; ++k) {
if (!(mask & (1 << k))) {
dp[i][mask] = max(dp[i][mask], p[i + b[k]] - p[i] + dfs(i + b[k], mask | (1 << k)));
}
}
return dp[i][mask] = max(dp[i][mask], dfs(i + 1, mask));
};
return dfs(0, 0);;
}
所有病人得到预约
n个病人,每个病人有两个喜欢的时间a[i]和b[i],可以在这两个时间的任意一个去看医生,医生有m个时间槽,编号1-m,有没有一种安排方式,所有病人都在自己喜欢的时间去看医生,且医生在每个时间槽最多只看一位病人。
- 1 <= n <= 1e6
- 1 <= m <= 2e6
- 1 <= a[i], b[i] <= m
- a[i] != b[i] for i = 1,..,n
分析
并查集,连接出现在同一病人喜欢的时间顶点,同一个连通图中出现的患者数量要不超过连通图中的时间节点数量。
bool isGoodArrange(vector<int> &a, vector<int> &b, int m) {
int n = a.size();
DSU d(m);
for (int i = 0; i < n; ++i) {
d.merge(a[i], b[i]);
}
vector<int> freq(m);
for (int i = 0; i < n; ++i) {
freq[d.get(a[i])]++;
}
for (int i = 0; i < n; ++i) {
if (d.size(a[i]) < freq[d.get(a[i])]) {
return false;
}
}
return true;
}
和相等的最多操作次数
给定长度为n的数组a,一次操作,可以删掉前两个、最后两个、或者最前面和最后面两个元素,每次操作的结果是删掉元素之和,求最多能操作多少次,使每次操作的结果都相等。
- 2 <= n <= 1000
- 1 <= a[i] <= 1e9
int max_op_nums(vector<int> &a) {
int n=sz(a);
ar3 b = {a[0]+a[1],a[0]+a[n-1],a[n-2]+a[n-1]};
vector<vector<ar3>> f(n,vector<ar3>(n));
f0(n-1){
int s=a[i]+a[i+1];
f2(j,3) if(s==b[j]) f[i][i+1][j]=1;
}
for(int l=3;l<=n;++l){
for(int i=0;i+l<=n;++i){
int j=i+l-1;
int s=a[i]+a[i+1];
for(int k=0;k<3;++k) {
if(s==b[k]) {
cmx(f[i][j][k],f[i+2][j][k]+1);
}
}
s=a[i]+a[j];
for(int k=0;k<3;++k) {
if(s==b[k]) {
cmx(f[i][j][k],f[i+1][j-1][k]+1);
}
}
s=a[j-1]+a[j];
for(int k=0;k<3;++k) {
if(s==b[k]) {
cmx(f[i][j][k],f[i][j-2][k]+1);
}
}
}
}
return max({f[0][n-1][0],f[0][n-1][1],f[0][n-1][2]});
}
appleoa
树中节点统计
给定n个节点的树,根结点是1,每个节点有个值,用数组a给出,对每个节点,统计如下两个值的和: 1.所有祖先节点中小于该节点值的和 2.所有祖先节点中大于该节点值的节点个数乘以当前节点的值
- 1 <= n <= 1e5
// 0 based
template <typename T>
struct Fenwick {
int n;
std::vector<T> a;
Fenwick(int n) : n(n), a(n) {}
void add(int x, T v) { // x: 1-based
for (int i = x; i <= n; i += i & -i) {
a[i - 1] += v;
}
}
T qry(int x) {
T ans = 0;
for (int i = x; i > 0; i -= i & -i) {
ans += a[i - 1];
}
return ans;
}
T qry(int l, int r) { //sum[l,..r] l,r: 1-based
if (l > r) return 0;
return qry(r) - qry(l - 1);
}
};
vector<long long> getValue(vector<int> &a, vector<vector<int>> &es) {
int n = a.size();
vector<long long> ans(n);
vector<vector<int>> g(n);
for(auto&e : es) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
Fenwick<long long> t1(n + 1), t2(n + 1);
auto v = a;
sort(v.begin(), v.end());
v.erase(unique(begin(v), end(v)), end(v));
auto get = [&](long long x) {
return lower_bound(v.begin(), v.end(), x) - v.begin() + 1;
};
function<void(int, int)> dfs = [&](int u, int fa) {
int t = get(a[u]);
long long x = t1.qry(1, t - 1), y = t2.qry(t + 1, n) * a[u];
ans[u] = x + y;
t1.add(t, a[u]);
t2.add(t, 1);
for (auto &v : g[u]) {
if (v == fa) continue;
dfs(v, u);
}
t1.add(t, -a[u]);
t2.add(t, -1);
};
dfs(0, -1);
return ans;
}
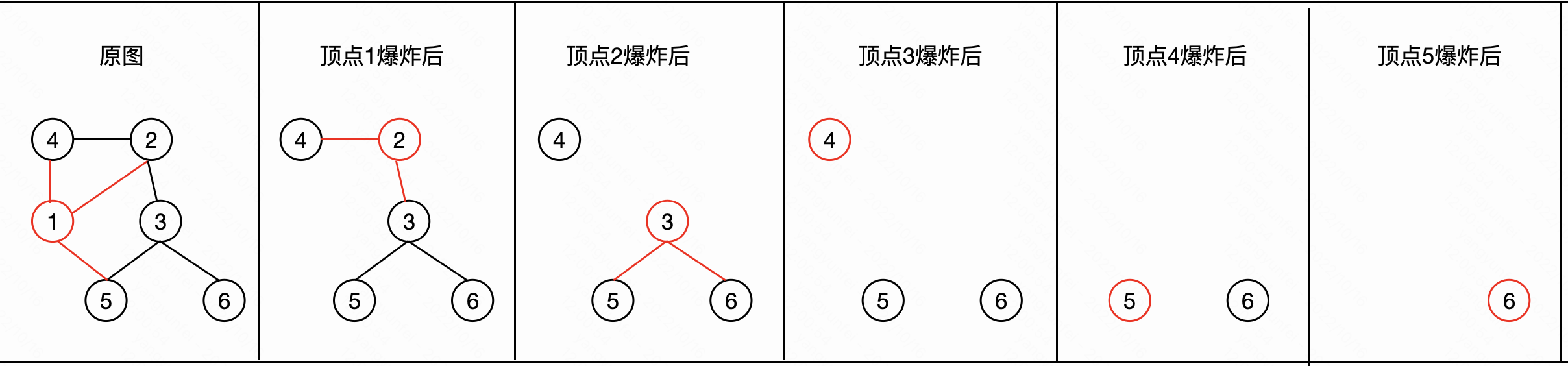
连通分量统计
n个点m条边的无向图,每个顶点有一个炸弹,炸弹会按照城市1到n的顺序依次爆炸,每次爆炸会销毁当前顶点以及所连接的边,对于每次爆炸,求爆炸后图中连通分量的数量。
- 1 <= n <= 2e5
- 0 <= m <= min(2e5,n(n-1)/2)
示例
input:
n = 6, m = 7
edges = [[1,2],[1,4],[1,5],[2,4],[2,3],[3,5],[3,6]]
output:
1 2 3 2 1 0
// DSU
vector<int> getComponent(int n, vector<vector<int>>& es) {
vector<vector<int>> g(n);
for (auto &e: es) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<int> ans(n), vis(n);
DSU d(n);
int t = 0;
for (int i = n - 1; i > 0; --i) {
t++;
for (auto &v : g[i]) {
if (vis[v] && !d.same(i, v)) {
t--;
d.merge(i, v);
}
}
ans[i - 1] = t, vis[i] = 1;
}
return ans;
}
树的切分方案数
n个点的树,树的值定义为树中所有节点的按位与之和,求满足下述条件的树的切分方案数目:
- 删除树中一条边,使得形成的两棵树的值相等。
- 2 <= n <= 1e5
- 1 <= a[i] <= 2^(31)-1
分析
设以节点0为根,维护如下两个数组:
- cnt[i]:以i为根的子树包含的节点个数
- s[i][j]:以i为根的子树包含的节点中第j位为1的个数
删除某条边e时,设其顶点为u,v,cnt[u]>cnt[v], 则可以求出以v为根节点的值,和剩余子树的值。
int treeSplit(vector<int> &a, vector<vector<int>> &es) {
int n = a.size(), ans = 0;
vector<vector<int>> g(n), s(n, vector<int>(32));
for (auto &e : es) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<int> cnt(n);
function<void(int, int)> dfs = [&](int u, int fa) {
cnt[u] = 1;
for (int i = 0; i < 32; ++i) if (a[u] & (1 << i))
s[u][i] = 1;
for (auto &v : g[u]) {
if (v == fa) continue;
dfs(v, u);
cnt[u] += cnt[v];
for (int i = 0; i < 32; ++i)
s[u][i] += s[v][i];
}
};
auto get = [&](vector<int> &p, int k) {
int x = 0;
for (int i = 0; i < 32; ++i) if (p[i] == k)
x = x | (1 << i);
return x;
};
dfs(0, -1);
for (auto &e : es) {
int u = e[0], v = e[1];
if (cnt[u] < cnt[v]) swap(u, v);
vector<int> c(32);
for (int i = 0; i < 32; ++i)
c[i] = s[0][i] - s[v][i];
if (get(c, cnt[0] - cnt[v]) == get(s[v], cnt[v])) ans++;
}
return ans;
}
树上询问
n个点的树(1-n),给个节点有一个值,1是根节点,q个询问,每个询问给定 (v, k) ,回答以v为根节点的子树中第k大数是多少?
- 2 <= n <= 1e5
- 0 <= a[i] <= 1e9
- 1 <= q <= 1e5
- 1 <= ki <= min(20, vi子树节点的数目)
input1:
n=5,q=2
es=[[1,4],[2,1],[2,5],[3,2]]
qs=[[1,2],[2,1]]
output:
4 5
vector<int> treeQuerys(vector<int> &a, vector<vector<int>> &es, vector<vector<int>> &qs) {
int n = a.size(), m = qs.size();
vector<vector<int>> g(n), s(n);
vector<priority_queue<int, vector<int>, greater<int>>> p(n);
for(auto& e: es) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
function<void(int, int)> dfs = [&](int u, int fa) {
p[u].push(a[u]);
for (auto &v : g[u]) {
if (v == fa) continue;
dfs(v, u);
auto q = p[v];
while(!q.empty()) {
p[u].push(q.top());
q.pop();
if(p[u].size() > 20) p[u].pop();
}
}
};
dfs(0, -1);
for (int i = 0; i < n; ++i) {
while(p[i].size()) {
s[i].push_back(p[i].top());
p[i].pop();
}
sort(rall(s[i]));
}
vector<int> ans(m);
for (int i = 0; i < m; ++i) {
int v = qs[i][0], k = qs[i][1];
ans[i] = s[v][k - 1];
}
return ans;
}
前缀得分
数组a的前缀子数组a[1..k] 的得分定义为:
- 对于 1 <= i <= k, 按顺序将当前前缀数组元素的最大值加到a[i]中
- a[k]的得分是 a[1..k]的最终元素的和
对于 k = 1,..n,计算a[i] 的得分,模 1e9+7
- 1 <= n <= 2e5
- 1 <= arr[i] <= 1e6
示例:
a = [1, 2, 3], ans = [0, 0, 0]
k = 1 时:
a[1..1] = [1]
mx(a[1..1]) = 1
new_array = [2]
ans[0] = sum(new_array) = 2
k=2时:
a[1..2] = [1,2]
mx(a[1..2]) = 2
new_array = [1 + 2, 2] -> [3, 2] -> [3, 2 + 3] -> [3, 5]
ans[1] = sum(new_array) = 8
k=3时:
a[1..3] = [1,2,3]
mx(a[1..3]) = 3
new_array = [4,2,3] -> [4, 6, 3] -> [4, 6, 9]
ans[2] = sum(new_array) = 19
分析
设s为a的前缀和数组,对于 i = k 时, mx = max(a[1..k]) 最终数组如下
a_new[1] = a[1] + mx = s[1] + mx a_new[2] = a_new[1] + a[2] = a[1] + a[2] + mx = s[2] + mx … a_new[k] = a_new[k - 1] + a[k] = s[k] + mx
vector<int> arrayScore(vector<int> &a) {
int n = a.size(), mod = 1e9 + 7;
vector<long long> p(n + 1);
for (int i = 0; i < n; ++i) {
p[i + 1] = p[i] + a[i];
}
vector<int> c(n);
long long s = 0, mx = 0;
for (int i = 0; i < n; ++i) {
mx = max(mx, (long long)a[i]);
s = (s + p[i + 1]) % mod;
c[i] = (s + (i + 1ll) * mx) % mod;
}
return c;
}
最小区间集合
给定n个闭区间,求最小的集合大小,使得每个区间都至少有两个数出现在集合中。
- 1 <= n <= 1e5
- 0 <= a[i][0] < a[i][1] < 1e9
分析
经典贪心
int miniIntervals(vector<vector<int>> &a) {
int n = a.size(), ans = 0, last = -1, pre = -1;
sort(a.begin(), a.end(), [&](auto &x, auto &y){
if (x[1] == y[1]) return x[0] > y[0];
return x[1] < y[1];
});
for (int i = 0; i < n; ++i) {
if (pre >= a[i][0]) continue;
else if (last >= a[i][0]) {
ans++, pre = last, last = a[i][1];
} else {
ans += 2, last = a[i][1], pre = last - 1;
}
}
return ans;
}
任意排列数组的最小绝对和
输入数组n和整数k,定义数组绝对和为 abs(a[i]-a[i+k]) 对于i=1,..n-k, 假设可以将数组a任意排列,求可能得到的最小绝对和。
- 2 <= n <= 3e5
- 1 <= k <= min(5000, n-1)
- -1e9 <= a[i] <= 1e9
分析
假设数组a=[a1,a2,…,an] 则要求的和为: abs(a[1]-a[k+1])+abs(a[2]+a[k+2])…+abs(a[n-k]-a[n]) 我们按模k将数组分成k组
a[1], a[k+1],..,a[i*k+1]...
a[2], a[k+2],..,a[i*k+2]...
...
a[k], a[k+k],..,a[j*k]...
在最优分组中,有两个结论
- 每个分组的元素都是原数组排序后相邻的一段,整个分组的绝对差之和即为该组最后一个元素减第一个元素。
- 每个组的元素数量要么为floor(n/k),要么为ceil(n/k),假设两者分别为n1和n2个。
问题转化为在一个排序数组中,将数组分成k段,其中n1段长为p,n2段长为(p+1),求绝对差之和的最小值.
设dp[i][j]:表示将数组分为i段长为p,j段长为(p+1)时的最优解。
时间复杂度 O(nlog(n) + k^2)
long long minSumPerm(vector<int> &a, int k) {
sort(a.begin(), a.end());
int n = a.size(), p1 = n / k, p2 = p1 + 1, n2 = n % k, n1 = k - n2;
vector dp(k + 1, vector<long long>(k + 1));
vector<long long> d(n + 1);
for (int i = 1; i < n; ++i) {
d[i] = d[i - 1] + a[i] - a[i - 1];
}
auto get = [&](int x, int y) {
return d[y - 1] - d[x - 1];
};
for (int i = 1; i <= n1; ++i) {
int x = i * p1, y = x - p1 + 1;
dp[i][0] = dp[i - 1][0] + get(y, x);
}
for (int i = 1; i <= n2; ++i) {
int x = i * p2, y = x - p2 + 1;
dp[0][i] = dp[0][i - 1] + get(y, x);
}
for (int i = 1; i <= n1; ++i) {
for (int j = 1; j <= n2; ++j) {
long long s = i * p1 + j * p2;
dp[i][j] = min(dp[i][j - 1] + get(s - p2 + 1, s), dp[i - 1][j] + get(s - p1 + 1, s));
}
}
return dp[n1][n2];
}
q次操作后的数组
长度为n的数组,q次操作,每次操作为下面两种类型之一
- 1 x 将数组中所有小于x的数变为x
- 2 i v 将 a[i] 赋值为v
- 1 <= n, q <= 1e6
- 1 <= a[i], x, v <= 1e9
分析
对于任意一个数a[i]
- 如果该位置没有赋值操作,设所有操作1中x的最大值为mx,则 a[i] = max(a[i], x)
- 否则,设最后一次赋值操作为第i次(第i次前的操作都会被覆盖),赋值为y,第i次后的操作1中的最大值为mx,则 a[i] = max(a[i], mx)
// ST
int op(int x,int y) {return max(x,y);}
vector<int> arrayQuerys(vector<int> a, vector<vector<int>>& qs) {
int n = a.size(), m = qs.size();
vector<int> p(m, -1), pos(n), ans = a;
for (int i = 0; i < m; ++i) {
if (qs[i][0] == 1) p[i] = qs[i][1];
else {
ans[qs[i][1]] = qs[i][2];
pos[qs[i][1]] = i;
}
}
ST<int,op> s1(p);
for (int i = 0; i < n; ++i) {
ans[i] = max(ans[i], s1.get(pos[i], m - 1));
}
return ans;
}
工作调度
有m个工作,n个处理器,如果相邻两个处理器处理的工作数目差不超过1,则称调度是平衡的,给定k (1<=k<=n),求满足第k个处理器处理数目最多且调度是平衡的 条件下,第k个处理器处理工作的最大值。
- 1 <= n <= 1e5
- n <= m <= 1e9
- 1 <= k <= n
long long arith_seq_sum(long long a1, long long d, long long n) {
return a1 * n + n * (n - 1) * d / 2;
}
int maxKthJob(int n, int m, int k) {
int l=1,r=m,c=l;
auto chk=[&](int x){
if(n*1ll*x<m)return 0;
long long s1=arith_seq_sum(x,-1,k+1)+arith_seq_sum(x,-1,n-k)-x;
if(s1>m)return 0;
return 1;
};
while(l<=r){
int md=(l+r)/2;
if(chk(md)){
c=md;l=md+1;
}else r=md-1;
}
return c;
}
void ac_yyf(int tt) {
int n,m,k;
cin>>n>>m>>k;
k--;
cout<<maxKthJob(n,m,k)<<nl;
}
树上或和
N个节点的树,带边权,每个节点有个值,用数组a给出,树中连通块的或和是同一个连通块中所有节点的值的或。 可以删除任意边,使得每个连通块中的节点的或和不小于B,求不能移除的节点中的边权最大值的最小可能值。
- 1 <= n <= 1e5
- 1 <= B, a[i], w[i] <= 1e6
// DSU
int tree_or_sum(vector<int> &a, vector<vector<int>> &es,int k) {
int n=sz(a);
int s=0,mx=0;
each(x,a)s|=x;
each(e,es){
cmx(mx,e[2]);
}
if(s<k)return -1;
auto chk=[&](int x){
DSU d(n);
for(auto&e:es){
if(e[2]<=x) d.merge(e[0],e[1]);
}
auto g=d.groups();
for(auto&v:g){
int o=0;
for(int x:v)
o|=a[x];
if(o<k)return 0;
}
return 1;
};
int l=0,r=mx,c=l;
while(l<=r){
int md=(l+r)/2;
if(chk(md)){
c=md;
r=md-1;
}else l=md+1;
}
return c;
}
包含t字符串的某个排列的子串数目
给定两个字符串s,t(均由小写字母组成),求s有多少个子串满足,t的某个排列至少在该子串中出现一次。
-
1 <= S <= 1e5 -
1 <= T <= 30
long long perm_str_count(string &s, string &t) {
int n=sz(s),m=sz(t);
vector<int> a(26),b(26);
for(auto&c:t)
a[c-'a']++;
vector<int> f(n),r(n,n);
f0(n){
b[s[i]-'a']++;
if(i>=m)b[s[i-m]-'a']--;
if(i>=m-1&&a==b)f[i-m+1]=1;
}
for(int i=n-1;i>=0;--i){
if(f[i])r[i]=i;
else if(i<n-1)r[i]=r[i+1];
}
long long c=0;
f0(n){
if(r[i]==n)continue;
c+=n-(r[i]+m-1);
}
return c;
}
获得目标字符串最少翻转次数
输入长为n二进制字符串s,初始全为0的二进制字符串t, 你可以对t进行一系列操作,每次操作可以选择一个下标x,翻转从x到n的所有字符(‘0’到’1’/’1’到’0’),求使t和s相等的最少操作次数。
int minFlips(string &s) {
char ch = '1';
int c = 0;
for (auto &x : s) {
if (x == ch) {
c++;
ch = ch ^ '1' ^ '0';
}
}
return c;
}
统计异或大于与pair
长度为n的数组,统计满足a[i]^a[j]>a[i]&a[j] 的(i,j)(i<j)对。
- 1 <= n <= 1e5
- 1 <= a[i] <= 1e9
long long xorGtandPair(vector<int> &a) {
const int K = 32;
int n = a.size(),c0=0;
vector<int> b(K);
long long c = 0;
for(auto&x:a){
if(x==0){
c0++;
continue;
}
int v=lg(x);
c+=b[v]++;
}
return n*1ll*(n-1)/2-c-c0*1ll*(c0-1)/2;
}
最大或和划分
给定长度为n的数组和整数k,将数组划分为k个连续子数组,使得每个子数组的按位或之和最大。
- 1 <= k <= n <= 5000
- 1 <= a[i] <= 2^30
// ST
int op(int x,int y) {return x|y;}
const int N = 5004;
int p[N][N];
long long f[N][N];
const ll inf=1e18;
long long max_or_sum(vector<int> &a, int K) {
int n=sz(a);
ST<int,op> s1(a);
f0(n)p[0][i]=0;
f[0][0]=a[0];
f1(n-1)f[0][i]=f[0][i-1]|a[i];
for(int k=1;k<K;++k){
p[k][n]=n;
for(int i=n-1;i>=k-1;--i){
int l=p[k-1][i],r=min(i,p[k][i+1]);
f[k][i]=-inf;
for(int j=r;j>=l;--j){
if (f[k][i] < f[k - 1][j - 1] + s1.get(j, i)){
f[k][i]=f[k-1][j-1]+s1.get(j, i);
p[k][i]=j;
}
}
}
}
return f[K-1][n-1];
}
统计数对
给定两个长为n的数组a,b,以及两个整数 x, y, 求同时满足如下条件的(i,j)对的数目
- 0 <= i < j < n
- a[i] + a[j] <= x
- b[i] + b[j] <= y
- 1 <= n <= 1e5
- 1 <= a[i], b[i], x, y <= 1e9
// FenwickTree
// Discrete
long long fancy_pairs(vector<int> &a,vector<int> &b, int k1, int k2){
int n=sz(a);
vector<pair<int,int> > p;
vector<int> c{k2};
f0(n){
p.emplace_back(a[i],b[i]);
}
sort(all(p));
for(auto&[x,y]:p){
if(y<=k2){
c.push_back(y);
c.push_back(k2-y);
}
}
Discrete<int> v(c);
int m=sz(v),j=n-1;
FenwickTree<int> f(m);
for(auto&[x,y]:p)if(y<=k2)
f.add(v(y),1);
long long s=0;
f0(n-1){
int x=p[i].first,y=p[i].second;
while(j>i&&x+p[j].first>k1){
if(p[j].second<=k2){
f.add(v(p[j].second),-1);
}
j--;
}
if(y<=k2) f.add(v(y),-1);
if(j<=i)break;
if(y>k2)continue;
s+=f.sum(0,v(k2-y));
}
return s;
}
树上每层最大异或和
一颗n个节点的树,每个节点有一个值,对树上每层的节点求异或和,假如求每层异或和时,你最多可以将该层的某个节点值和任意节点值交换,求每层能获得的最大异或和。每次交换不改变原树,即每层都在原始树上进行交换和求值。
- 1 <= n <= 2e5
- 1 <= a[i] <= 1e9
const int N = 2e5 + 4, K = 30, M = K * N;
int tr[M][2], idx, cnt[M];
void add(int x) {
int p = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
if (!tr[p][b]) tr[p][b] = ++idx;
cnt[p = tr[p][b]]++;
}
}
void del(int x) {
int p = 0;
for (int i = K - 1; ~i; --i)
cnt[p = tr[p][(x >> i) & 1]]--;
}
int query(int x) {
int p = 0, ans = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
ans = ans << 1;
if (cnt[tr[p][b]]) ans++, p = tr[p][b];
else p = tr[p][!b];
}
return ans;
}
vector<int> max_level_sum(vector<vector<int>> &es, vector<int> &a) {
int n=sz(a);
idx=0;
memset(tr,0,sizeof(int)*K*(n+1)*2);
memset(cnt,0,sizeof(int)*K*(n+1));
vector<vector<int>> g(n);
for(auto&e:es){
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
int mx=0;
vector<int> dep(n);
function<void(int, int)> dfs = [&](int u, int fa) {
cmx(mx,dep[u]);
for(auto&v:g[u])if(v!=fa){
dep[v]=dep[u]+1;
dfs(v,u);
}
};
dfs(0, -1);
vector<vector<int>> p(mx+1);
f0(n){
add(a[i]);
p[dep[i]].push_back(i);
}
vector<int> c(mx+1);
f0(mx+1){
int cu=0,mx;
for(auto&x:p[i])
cu^=a[x];
mx=cu;
for(auto&x:p[i]){
cu^=a[x];
cmx(mx,query(~cu));
cu^=a[x];
}
c[i]=mx;
}
return c;
}
xor_subsequence
输入数组a,构造一个子序列b,满足 1: b[i]< b[i+1] for 1 <= i < |b|
- pct(b[1]^..^b[i]) <= pct(b[i+1])
- 1 <= |a| <= 1e5 1 1 <= a[i] <= 100
设x为b中所有元素的异或和,求x的所有可能的不同取值数量。
int xor_subsequence(vector<int> &a) {
vector<int> c(128, -1);
for (int x : a) {
for (int y = 0; y < 128; ++y) if (c[y] != -1) {
if (c[y] < x && pct(y) <= pct(x)) {
int k = x ^ y;
if (c[k] == -1 || x < c[k]) c[k] = x;
}
}
}
int ans = 0;
for (int x : c)
ans += c != -1;
return ans;
}
选择元素之和
输入长度为n的数组a,和m,按照下面操作选择元素,求所选元素之和。
- 选择处于前k个元素或后k个元素中的最大值(最多会有2k个,值相同选最小下标)
- 将所选元素删除,继续步骤1,直到选择m个元素。 如果元素少于k个,则所有元素都是可选择的。
- 1 <= m, k <= n <= 1e5
- 1 <= a[i] <= 1e9
4段子数组最大差值
一个长度为n的数组a,将a划分为4段(可以为空),数组中每个元素恰好属于其中一段,设划分为 a=s1s2s3s4,求s1+s3-(s2+s4)的最大值。
- 1 <= n <= 1e5
- -1e9 <= a[i] <= 1e9
ll max_subarr_diff(vector<int> &a) {
int n=sz(a);
ll sm=Sm(a), s1=0, mn=1e18;
vector<long long> p(n+1), s(n+1);
for(int i=0;i<n;++i)
s[i+1]=min((ll)a[i],a[i]+s[i]);
for(int i=n-1;i>=0;--i){
s1+=a[i];
p[i]=min(s1,p[i+1]);
}
f0(n+1){
cmn(p[i],0);
cmn(s[i],0);
}
for(int i=0;i<n;++i)
cmn(mn,p[i+1]+s[i+1]);
return sm-2*mn;
}





