===
Index
模板
template <typename T, int bit_len = numeric_limits<make_unsigned_t<T>>::digits>
class XorTrie {
using U = make_unsigned_t<T>;
struct Node {
int siz;
Node *ch[2] {nullptr, nullptr};
Node() : siz(0) {}
~Node() { delete ch[0]; delete ch[1];}
inline Node* get_or_new(bool b) noexcept { if (is_absent(b)) ch[b] = new Node(); return ch[b];}
inline Node* operator[](bool b) const noexcept { return ch[b]; }
inline bool is_absent (bool b) const noexcept { return ch[b] == nullptr; }
inline bool is_present(bool b) const noexcept { return ch[b] != nullptr; }
static inline int size(const Node *const node) noexcept { return node == nullptr ? 0 : node->siz; }
inline void update_size() noexcept { siz = size(ch[0]) + size(ch[1]); }
};
public:
XorTrie() : root(new Node) {}
~XorTrie() { delete root; }
inline int size() const noexcept { return Node::size(root); }
inline bool empty() const noexcept { return size() == 0; }
int add(const U val, const int num = 1) noexcept {
if (num == 0) return 0;
Node *cur = root;
cur->siz += num;
for (int i = bit_len; i --> 0;) {
cur = cur->get_or_new(bit(val, i));
cur->siz += num;
}
return cur->siz;
}
int del(const U val, const int num = 1) noexcept {
if (num == 0) return 0;
return del(root, bit_len - 1, val, num);
}
int clear(const U val) noexcept { return del(val, numeric_limits<int>::max());}
int prefix_count(const U val, const unsigned int l) const noexcept {
Node *cur = root;
for (int i = bit_len; i --> l;) {
if (cur == nullptr) return 0;
cur = (*cur)[bit(val, i)];
}
return Node::size(cur);
}
inline int count(const U val) const noexcept { return prefix_count(val, 0); }
inline bool contains(const U val) const noexcept { return count(val) > 0; }
inline U xor_kth_min(const U x, const int k) const {
assert(0 <= k and k < size());
return xor_kth_ele<false>(x, k);
}
inline U xor_kth_max(const U x, const int k) const {
assert(0 <= k and k < size());
return xor_kth_ele<true>(x, k);
}
inline U xor_min(const U x) const { return xor_kth_min(x, 0); }
inline U xor_max(const U x) const { return xor_kth_max(x, 0); }
int xor_count_lt(const U x, const U val) const noexcept {
int res = 0;
Node *cur = root;
for (int i = bit_len - 1; i >= 0; --i) {
if (cur == nullptr) break;
bool bx = bit(x, i);
bool bv = bit(x ^ val, i);
if (bx != bv) {
res += Node::size((*cur)[bx]);
}
cur = (*cur)[bv];
}
return res;
}
inline int xor_count_leq(const U x, const U val) const noexcept { return xor_count_lt(x, val) + count(val); }
inline int xor_count_gt (const U x, const U val) const noexcept { return size() - xor_count_leq(x, val); }
inline int xor_count_geq(const U x, const U val) const noexcept { return size() - xor_count_lt(x, val); }
inline U xor_lower(const U x, const U val, const U default_value = ~U(0)) const noexcept {
int k = size() - xor_count_geq(x, val) - 1;
return k < 0 ? default_value : xor_kth_ele(x, k);
}
inline U xor_floor(const U x, const U val, const U default_value = ~U(0)) const noexcept {
int k = size() - xor_count_gt(x, val) - 1;
return k < 0 ? default_value : xor_kth_ele(x, k);
}
inline U xor_higher(const U x, const U val, const U default_value = ~U(0)) const noexcept {
int k = xor_count_leq(x, val);
return k == size() ? default_value : xor_kth_ele(x, k);
}
inline U xor_ceil(const U x, const U val, const U default_value = ~U(0)) const noexcept {
int k = xor_count_lt(x, val);
return k == size() ? default_value : xor_kth_ele(x, k);
}
inline U kth_min(const int k) const { return xor_kth_min(0, k); }
inline U min() const { return xor_kth_min(0, 0); }
inline U max() const { return xor_kth_min(~U(0), 0); }
inline int count_lt (const U val) const noexcept { return xor_count_lt(0, val); }
inline int count_leq(const U val) const noexcept { return xor_count_leq(0, val); }
inline int count_gt (const U val) const noexcept { return xor_count_gt(0, val); }
inline int count_geq(const U val) const noexcept { return xor_count_geq(0, val); }
inline U lower (const U val, const U default_value = ~U(0)) const noexcept { return xor_lower (0, val, default_value); }
inline U floor (const U val, const U default_value = ~U(0)) const noexcept { return xor_floor (0, val, default_value); }
inline U higher(const U val, const U default_value = ~U(0)) const noexcept { return xor_higher(0, val, default_value); }
inline U ceil (const U val, const U default_value = ~U(0)) const noexcept { return xor_ceil (0, val, default_value); }
private:
Node *const root;
static constexpr bool bit(const U x, const int i) noexcept { return (x >> i) & 1;}
int del(Node *cur, const int k, const U val, const int num) {
if (k == -1) {
int removed = std::min(cur->siz, num);
cur->siz -= removed;
return removed;
}
bool b = bit(val, k);
if (cur->is_absent(b)) return 0;
int removed = del((*cur)[b], k - 1, val, num);
cur->update_size();
return removed;
}
template <bool is_max_query = false>
U xor_kth_ele(const U x, const int k) const noexcept {
U res = 0;
int rest = k;
Node *cur = root;
for (int i = bit_len - 1; i >= 0; --i) {
bool b = is_max_query ^ bit(x, i);
int sz = Node::size((*cur)[b]);
if (sz <= rest) rest -= sz, b = not b;
res |= U(b) << i;
cur = (*cur)[b];
}
return x ^ res;
}
};
使用方法
- 定义 trie
XorTrie<int, 30> t;
2.统计与x异或小于k的数目
t.xor_count_lt(x, k)
数组模板
// N是元素个数,K是每个元素最大的长度,int不超过32位。
const int N = 1e5 + 10, K = 32, M = K * N;
int tr[M][2], idx, cnt[M];
void add(int x) {
int p = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
if (!tr[p][b]) tr[p][b] = ++idx;
cnt[p = tr[p][b]]++;
}
}
void del(int x) {
int p = 0;
for (int i = K - 1; ~i; --i)
cnt[p = tr[p][(x >> i) & 1]]--;
}
int query(int x) {
int p = 0, ans = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
ans = ans << 1;
if (cnt[tr[p][b]]) ans++, p = tr[p][b];
else p = tr[p][!b];
}
return ans;
}
最大异或对
求n个整数任意两个元素的异或和的最大值。
- 1 <= n <= 1e5
- 1 <= a[i] < 2^31
时间复杂度 O(n * k), k是二进制的长度, 一般不超过32
// XorTrie
int main() {
int n,ans = 0, x;
XorTrie<int, 31> t;
scanf("%d",&n);
for (int i = 0; i < n; ++i) {
scanf("%d",&x);
if (i > 0) ans = max(ans, (int)t.xor_max(x));
t.add(x);
}
printf("%d\n", ans);
return 0;
}
树上最大异或值路径
给定一个树,树上的边都具有权值。 树中一条路径的异或长度被定义为路径上所有边的权值的异或和 给定上述的具有 n 个节点的树,你能找到异或长度最大的路径吗?
输入格式
- 第一行包含整数 n,表示树的节点数目。
- 接下来 n−1 行,每行包括三个整数 u,v,w,表示节点 u 和节点 v 之间有一条边权重为 w。
输出格式
- 输出一个整数,表示异或长度最大的路径的最大异或和。
数据范围
- 1 <= n <= 100000
- 0 <= u, v < n
- 0 <= w < 2^31
分析
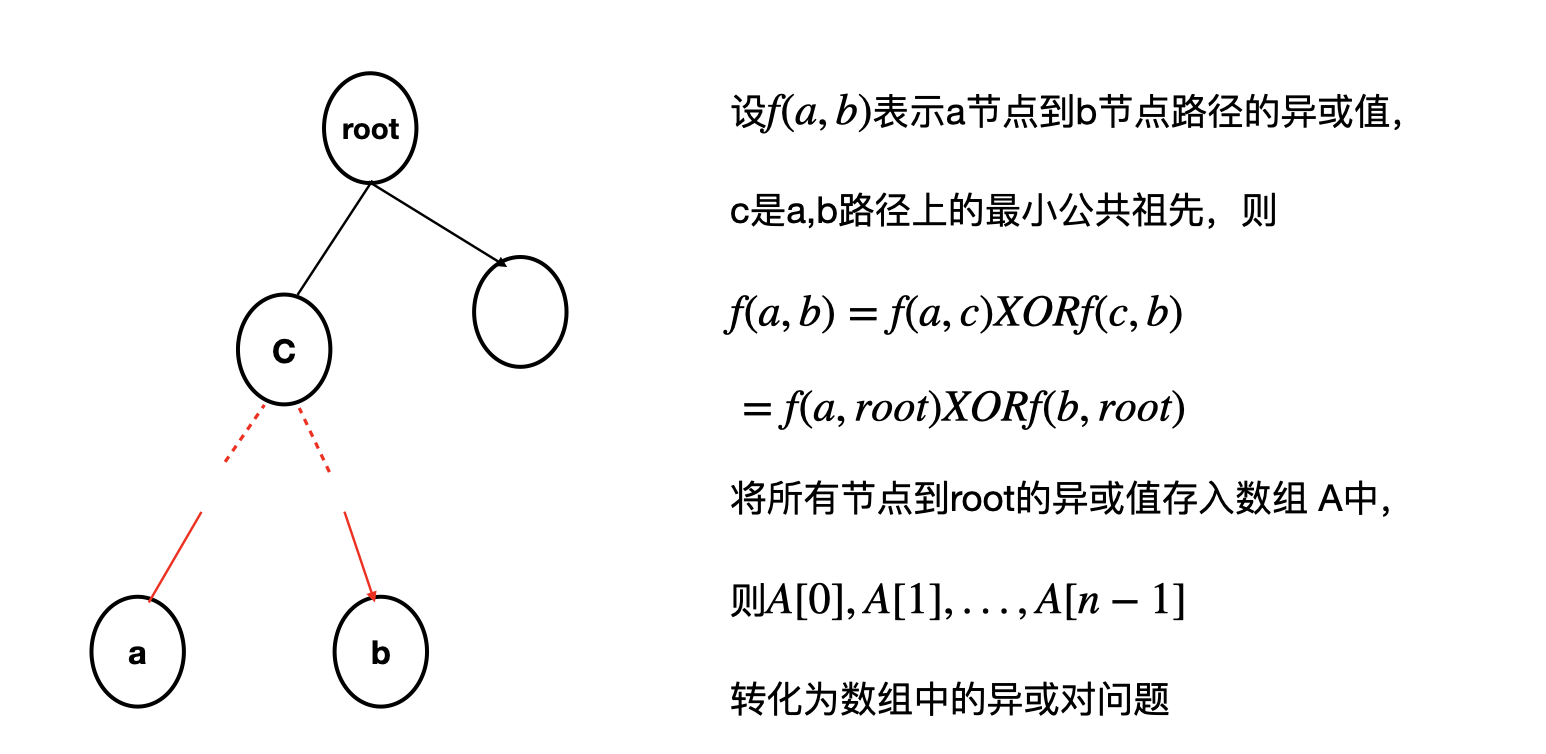
#include <bits/stdc++.h>
using namespace std;
//模板
int a[N], n, u, v, w;
vector<pair<int,int>> G[N];
void dfs(int u, int fa, int sum) {
a[u] = sum;
for (auto v : G[u]) {
if (v.first != fa) {
dfs(v.first, u, sum ^ v.second);
}
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n - 1; i ++ ) {
scanf("%d%d%d", &u, &v, &w);
G[u].push_back({v,w});
G[v].push_back({u,w});
}
dfs(0, -1, 0);
int ans = 0;
XorTrie<int,31> t;
for (int i = 0; i < n; i ++ ) {
if (i) ans = max(ans, (int)t.xor_max(a[i]));
t.add(a[i]);
}
printf("%d\n",ans);
}
统计异或值在范围内的数对有多少
给你一个整数数组 nums (下标 从 0 开始 计数)以及两个整数:low 和 high ,请返回 漂亮数对 的数目。
漂亮数对 是一个形如 (i, j) 的数对,其中 0 <= i < j < nums.length 且 low <= (nums[i] XOR nums[j]) <= high 。
提示
- 1 <= nums.length <= 2 * 10^4
- 1 <= nums[i] <= 2 * 10^4
- 1 <= low <= high <= 2 * 10^4
// XorTrie
class Solution {
public:
int countPairs(vector<int>& a, int l, int h) {
XorTrie<int,15> t;
int ans=0;
for(int i:a){
ans += t.xor_count_lt(i,h + 1) - t.xor_count_lt(i,l);
t.add(i);
}
return ans;
}
};
数对异或和
给一个长度为n的数组,a[0], a[1], … a[n-1].
求所有满足 1<=i<j<=N 的pair(i,j),其a[i]^a[j]的和对1e9+7取模的结果。
数据范围
- 2 <= N <= 3e5
- 0 <= a[i] < 2**60
- a[i] 是整型
分析
由于采取异或操作时,各个bit互不影响,因此可以每个bit独立计算,
对于第k位,只有a[i]和a[j]在第k位不同,其异或值才为1,否则为0,
因此,第k位异或值为1的数对 数目等于 (n个数中第k位为1的数目)* (n个数中第k位为0的数目)
所以只需求出每一位中为1和为0的数量,时间复杂度为O(N*log(max(a[i])))
#include <bits/stdc++.h>
using namespace std;
const int P = 1e9 + 7;
int main() {
int n;
cin >> n;
vector<long long> a(n);
for (int i = 0; i < n; ++i)
cin >> a[i];
long long ans = 0;
for (int k = 0; k < 60; ++k) {
int c[2] = {};
for (int i = 0; i < n; ++i)
++c[a[i] >> k & 1];
ans = (ans + (1LL << k) % P * c[0] % P * c[1]) % P;
}
cout << ans << endl;
return 0;
}
数对最短距离异或和
一个包含n个点,n-1条无向边的无环图(树),第i条边连接 u[i] 和v[i],具有权重w[i], 对于顶点对(x,y),定义 dist(x,y) = 从x到y最短路径上的权重异或值。
对于所有满足 1<=i<j<=N 的顶点对(i,j),,求dist(i,j)的和对1e9+7取模的结果。
数据范围
- 2 <= N <= 2e5
- 1 <= u[i] < v[i]
- 0 <= w[i] < 2**60
- 输入图是棵树
- 所有数值都是整型
分析
首先化简dist(i,j), 随意选择一个节点作为根,设为 x, 设k是i,j的最近公共祖先,则dist(i,j)满足如下性质:
dist(i,j) = dist(k, i) ^ dist(k, j)
继续化简
dist(i, j) = dist(k, i) ^ dist(k, j)
= dist(k, i) ^ dist(k, j) ^ dist(x, k) ^ dist(x, k)
= (dist(x, k) ^ dist(k, i)) ^ (dist(x, k) ^ dist(k, j))
= dist(x, i) ^ dist(x, j)
问题转化为 对于所有满足 1<=i<j<=N 的顶点对(i,j),,求dist(x, i) ^ dist(x, j)的和对1e9+7取模的结果。
对于每一个dist(x, i),我们可以在O(N)时间内使用BFS求出每一个节点与x的dist值,将其存到数组里,问题则转化为上一题。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll mod = 1e9+7;
int main(){
int N; cin >> N;
vector<vector<ll>> edge(N), weight(N);
for(int i=1; i<N; i++){
ll u,v,w; cin >> u >> v >> w; u--, v--;
edge[u].push_back(v);
edge[v].push_back(u);
weight[u].push_back(w);
weight[v].push_back(w);
}
vector<ll> dist(N,-1);
queue<int> que;
que.push(0);
dist[0] = 0;
while(!que.empty()){
int now = que.front(); que.pop();
for(int i=0; i<edge[now].size(); i++){
int next = edge[now][i];
ll sum = dist[now]^weight[now][i];
if(dist[next] == -1){
dist[next] = sum;
que.push(next);
}
}
}
ll ans = 0;
for(int i=0; i<60; i++){
vector<int> cnt(2);
for(int j=0; j<N; j++) cnt[dist[j]>>i&1]++;
ans += (1ll<<i)%mod*cnt[0]%mod*cnt[1];
ans %= mod;
}
cout << ans << endl;
}
奶牛排队
又一个长度为n的数组,a[1],…,a[n], 从数组中选取一个子数组,使得子数组的异或和最大。
如果有多个这样的子数组,选择结尾下标最小的,如果还不唯一,选择最短的。
输出 :最大的异或值,序列的起始位置、终止位置。
- 1 <= n <= 1e5
- 0 <= a[i] <= 2^21 - 1
分析
对于区间的问题,我们希望转化成和两个端点相关的问题去做, 区间[l,r]的异或和等于前r个数的异或和和前l-1个数的异或和异或,所以,我们只需要在前缀异或和数组里面任选两个数让他们异或和最大即可,
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, K = 23, M = K * N;
int tr[M][2], idx, id[M];
void add(int x, int k) {
int p = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
if (!tr[p][b]) tr[p][b] = ++idx;
p = tr[p][b];
}
id[p] = k;
}
int query(int x, int &y) {
int p = 0, ans = 0;
for (int i = K - 1; ~i; --i) {
int b = (x >> i) & 1;
if (tr[p][!b]) ans |= 1 << i, p = tr[p][!b];
else p = tr[p][b];
}
y = id[p];
return ans;
}
int s[N], x, y, n;
int main(){
scanf("%d",&n);
add(0,0);
int ans = 0, l = 1, r = 1;
for (int i = 1; i <= n; ++i) {
scanf("%d", &s[i]);
s[i] ^= s[i - 1];
x = query(s[i], y);
if (x > ans) ans = x, l = y + 1, r = i;
add(s[i], i);
}
printf("%d %d %d\n", ans,l,r);
}
xor-mst
n个节点的完全无向图,每个节点有个值a[i],任意两点的边权为 a[i]^a[j], 求图最小生成树的权重和。‘
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N = 200100, M = N * 31;
int tr[M][2], idx = 1, mx[M], a[N], n;
ll gans=0;
void add(int x, int c) {
int p = 0;
for (int i = 29; i >= 0; --i) {
mx[p] = max(mx[p], c);
int g = (x >> i) & 1;
if (tr[p][g])
p = tr[p][g];
else
p = tr[p][g] = idx++;
}
mx[p] = max(mx[p], c);
}
int query(int x, int b) {
int p = 0, ans = 0;
for (int i = 29; ~i; --i) {
int u = (x >>i) & 1;
if (tr[p][u] && mx[tr[p][u]] >= b)
p = tr[p][u];
else p = tr[p][!u], ans += (1 << i);
}
return ans;
}
void run(int l, int r, int k) {
if (l + 1 >= r || k < 0)
return;
int mid = l;
while (mid < r && !((a[mid] >> k) & 1))
++mid;
run(l, mid, k - 1);
run(mid, r, k - 1);
if (mid == l || mid == r)
return;
int ans = (1 << 30) + 100;
for (int i = l; i < mid; ++i)
ans = min(ans, query(a[i], mid));
gans += ans;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%d", a + i);
sort(a, a + n);
for (int i = 0; i < n; ++i)
add(a[i], i);
run(0, n, 29);
cout << gans << "\n";
return 0;
}
排列异或和
codechef 2022 january lunchtime
给一个n, 在1-n的所有排列中,求 (1^p1)+(2^p2)+…+(n^pn)的最大和
long long maxXorSum(int n) {
long long ans = 0;
for (int i = 0; i < 30; ++i) {
int cnt = 0;
if (n >= (1 << i)) {
cnt += max(0, n % (1 << (i+1)) + 1 - (1 << i));
cnt += n >> (i + 1) << i;
}
if (cnt * 2 <= n) cnt = cnt * 2;
else cnt = (n - cnt) * 2;
ans += (long long ) cnt << i;
}
return ans;
}
可持久化01trie
对于查询[0,n]的最大异或和问题,可以使用01trie,对于查询任意区间的最大异或和问题,需要使用可持久化01trie。 注意,设元素总数为n,当查询右边界取到n时可能出现问题,为了避免查询时右边界取到最后一个元素出现异常, 在add完所有元素时,需要手动再添加一个0.
模板
const int N = 2e5 + 4, K = 24, M = K * N;
int tr[M][2], rt[N], sum[M], idx, tot;
void add(int x) {
int p = rt[idx];
rt[++idx] = tot + 1;
for (int i = K - 1; ~i; --i) {
sum[++tot] = sum[p] + 1;
bool b = x & (1 << i);
tr[tot][b] = tot + 1, tr[tot][!b] = tr[p][!b];
p = tr[p][b];
}
}
int query(int l, int r, int x) {
if (l > r) return 0;
l = rt[l], r = rt[r];
int ans = 0;
for (int i = K - 1; ~i; --i) {
bool b = x & (1 << i);
if (sum[tr[r][!b]] - sum[tr[l][!b]])
ans += (1 << i), l = tr[l][!b], r = tr[r][!b];
else
l = tr[l][b], r = tr[r][b];
}
return ans;
}
区间最大异或和
给定一个非负整数序列 a,初始长度为 N。
有 M 个操作,有以下两种操作类型:
- A x:添加操作,表示在序列末尾添加一个数 x,序列的长度 N 增大 1。
-
Q l r x:询问操作,你需要找到一个位置 p,满足 l≤p≤r,使得:a[p] ^ a[p+1] ^ … ^ a[N] ^ x 最大,输出这个最大值。
- 0 < n,m <= 3e5
- 0 <= a[i] <= 1e7
分析
维护前缀异或,a[p]^...^a[n] = s[p-1]^s[n]
#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 4, K = 24, M = K * N;
int tr[M][2], rt[N], sum[M], idx, tot;
void add(int x) {
int p = rt[idx];
rt[++idx] = tot + 1;
for (int i = K - 1; ~i; --i) {
sum[++tot] = sum[p] + 1;
bool b = x & (1 << i);
tr[tot][b] = tot + 1, tr[tot][!b] = tr[p][!b];
p = tr[p][b];
}
}
int query(int l, int r, int x) {
if (l > r) return 0;
l = rt[l], r = rt[r];
int ans = 0;
for (int i = K - 1; ~i; --i) {
bool b = x & (1 << i);
if (sum[tr[r][!b]] - sum[tr[l][!b]])
ans += (1 << i), l = tr[l][!b], r = tr[r][!b];
else
l = tr[l][b], r = tr[r][b];
}
return ans;
}
int n,m,x,y,k,q;
int main(){
scanf("%d%d",&n,&m);
add(0); y = 0;
for(int i=0;i<n;++i){
scanf("%d",&x);
add(y^=x);
}
while(m--){
char op[4];
scanf("%s",op);
if(op[0]=='A'){
scanf("%d",&x);
add(y^=x);
}else{
int l,r,x;
scanf("%d%d%d",&l,&r,&x);
cout<<query(l-1,r,y^x)<<"\n";
}
}
return 0;
}
查询区间最大异或
长度为n的数组,q次询问,每次询问给定l,r,x,求区间[l,r]内元素与x异或值的最大值是多少。
- 1 <= n <= 3e5
- 1 <= q <= 1e5
- 1 <= l <= r <= n
- 1 <= a[i], x <= 1e6
const int N = 3e5+2, K = 20, M = K * N;
// xxx
vector<int> max_xor_query(vector<int> &a, vector<vector<int>> &qs){
int n=sz(a),q=sz(qs);
each(x,a)add(x); add(0); //最后加个add(0)
vector<int> ans(q);
f0(q){
ans[i]=query(qs[i][0],qs[i][1]+1,qs[i][2]);
}
return ans;
}
void solve(int tt) {
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
rd(q);
vector<vector<int>> qs(q,vector<int>(3));
f0(q){
int u,v,w;
rd(u,v,w);
u--,v--;
qs[i]={u,v,w};
}
auto ans=max_xor_query(a,qs);
each(x,ans)wt(x,nl);
}
树上路径最大异或和
n个节点的树,每天边有边权,q次查询,每次查询给定u,v,x 求u,v路径上的边权与x异或的最大值是多少。
- 2 <= n, q <= 1e5
- 1 <= w, x <= 1e6
分析
与上题类似,需要使用HLD将树上路径转化为多个区间,HLD需要将边权转点权。
// HLD 边权转点权
// const int N = 1e5+2, K = 20, M = K * N;
vector<int> xor_path_query(int n, vector<vector<int>> &es, vector<vector<int>> &qs) {
HLD g(n);
for(auto&e:es){
g.add_edge(e[0],e[1]);
}
g.build();
vector<int> a(n);
for(auto&e:es){
int u=e[0],v=e[1],w=e[2];
if(g.dep[u]>g.dep[v])swap(u,v);
a[g.in[v]]=w;
}
each(x,a)add(x);add(0); //最后需要再add(0)
vector<int> ans(q);
f0(q){
int u=qs[i][0],v=qs[i][1],w=qs[i][2];
int s=0;
g.path(u,v,[&](int x, int y){
cmx(s,query(x,y,w));
});
ans[i]=s;
}
return ans;
}





