leetcode会员题

2021-04-12 | 阅读：次

===

Index

683.K 个关闭的灯泡
681.最近时刻
1057.校园自行车分配
642. 设计搜索自动补全系统
271. 字符串的编码与解码
723. 粉碎糖果
727. 最小窗口子序列
772. 中缀表达式求值
1153. 字符串转化
361. 轰炸敌人
317. 离建筑物最近的距离
1231. 分享巧克力
774. 最小化去加油站的最大距离

k个关闭的灯泡

N 个灯泡排成一行，编号从 1 到 N 。最初，所有灯泡都关闭。每天只打开一个灯泡，直到 N 天后所有灯泡都打开。给你一个长度为 N 的灯泡数组 blubs ，其中 bulls[i] = x 意味着在第 (i+1) 天，我们会把在位置 x 的灯泡打开，其中 i 从 0 开始，x 从 1 开始。

给你一个整数 K ，请你输出在第几天恰好有两个打开的灯泡，使得它们中间正好有 K 个灯泡且这些灯泡全部是关闭的。如果不存在这种情况，返回 -1 。如果有多天都出现这种情况，请返回最小的天数。

数据说明

1 <= N <= 20000
1 <= bulbs[i] <= N
bulbs 是一个由从 1 到 N 的数字构成的排列
0 <= K <= 20000

示例

输入：
bulbs: [1,3,2]
K: 1
输出：2
解释：
第一天 bulbs[0] = 1，打开第一个灯泡 [1,0,0]
第二天 bulbs[1] = 3，打开第三个灯泡 [1,0,1]
第三天 bulbs[2] = 2，打开第二个灯泡 [1,1,1]
返回2，因为在第二天，两个打开的灯泡之间恰好有一个关闭的灯泡。

解答

利用set的有序性，每次打开一个灯泡时，看与其相邻位置的两个开着的灯泡和当前灯泡距离是否为k

    int kEmptySlots(vector<int>& bulbs, int k) {
        int n = bulbs.size();
        set<int> s;
        for (int i = 0; i < n; ++i) {
            int x = bulbs[i];
            auto it = s.insert(x).first;
            auto pre = it, next = it;
            if (pre != s.begin()) pre--;
            if (next != s.end()) next++;
            if(x - *pre == k + 1 || *next - x == k + 1) 
                return i + 1;
        }
        return -1;
    }

校园自行车分配

在由 2D 网格表示的校园里有 n 位工人（worker）和 m 辆自行车（bike），n <= m。所有工人和自行车的位置都用网格上的 2D 坐标表示。

我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中，我们选取彼此之间曼哈顿距离最短的工人自行车对 (worker, bike) ，并将其中的自行车分配給工人。如果有多个 (worker, bike) 对之间的曼哈顿距离相同，那么我们选择工人索引最小的那对。类似地，如果有多种不同的分配方法，则选择自行车索引最小的一对。不断重复这一过程，直到所有工人都分配到自行车为止。

给定两点 p1 和 p2 之间的曼哈顿距离为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。

返回长度为 n 的向量 ans，其中 a[i] 是第 i 位工人分配到的自行车的索引（从 0 开始）。

class Solution {
public:
    struct Node {
        int wi, bi, d;
        bool operator < (const Node& rth) const {
            if (d < rth.d) return 0;
            if (d == rth.d && wi < rth.wi) return 0;
            if (d == rth.d && wi == rth.wi && bi < rth.bi) return 0;
            return 1;
        }
    };
    vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int n = workers.size(), m = bikes.size();
        priority_queue<Node> pq;
        vector<int> ws(n), bs(m), res(n);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int d = abs(workers[i][0]-bikes[j][0]) + abs(workers[i][1]-bikes[j][1]);
                pq.push({i, j, d});
            }
        }
        int cnt = 0;
        while(cnt < n) {
            auto t = pq.top(); pq.pop();
            if (ws[t.wi] || bs[t.bi]) continue;
            ws[t.wi] = bs[t.bi] = 1;
            cnt++;
            res[t.wi] = t.bi;
        }
        return res;
    }
};

设计搜索自动补全系统

为搜索引擎设计一个搜索自动补全系统。用户会输入一条语句（最少包含一个字母，以特殊字符 ‘#’ 结尾）。除 ‘#’ 以外用户输入的每个字符，返回历史中热度前三并以当前输入部分为前缀的句子。下面是详细规则：

一条句子的热度定义为历史上用户输入这个句子的总次数。返回前三的句子需要按照热度从高到低排序（第一个是最热门的）。如果有多条热度相同的句子，请按照 ASCII 码的顺序输出（ASCII 码越小排名越前）。如果满足条件的句子个数少于 3，将它们全部输出。如果输入了特殊字符，意味着句子结束了，请返回一个空集合。

你的工作是实现以下功能：

构造函数：

AutocompleteSystem(String[] sentences, int[] times): 这是构造函数，输入的是历史数据。 Sentences 是之前输入过的所有句子，Times 是每条句子输入的次数，你的系统需要记录这些历史信息。

现在，用户输入一条新的句子，下面的函数会提供用户输入的下一个字符：

List input(char c): 其中 c 是用户输入的下一个字符。字符只会是小写英文字母（'a' 到 'z' ），空格（' '）和特殊字符（'#'）。输出历史热度前三的具有相同前缀的句子。

struct Node{
    string str;
    int count;
    unordered_map<char,Node*> words;
};

class Trie{
public:
    Node* root;
    Trie(){root = new Node();}
    
    void insert(string& input, int time){
        Node* curr = root;
        for(char ch: input){
            if(curr->words.find(ch) == curr->words.end()){
                curr->words[ch] = new Node();
            }
            curr = curr->words[ch];
        }
        curr->count += time;
        curr->str = input;
    }
    
    void search(Node* curr, vector<pair<int,string>> &results){
        if(!curr) return;
        if(curr->count > 0){
            results.push_back(make_pair(-curr->count, curr->str));
        }
        for(auto& p: curr->words){
            search(p.second, results);
        }
    }
};

class AutocompleteSystem {
public:
    AutocompleteSystem(vector<string>& sentences, vector<int>& times) {
        trie = new Trie();
        currInput.clear();
        for(int i = 0; i < sentences.size(); ++i){
            trie->insert(sentences[i], times[i]);
        }
        node = trie->root;
    }
    
    vector<string> input(char c) {
        vector<string> res;
        if(c == '#'){
            trie->insert(currInput, 1);
            currInput.clear();
            node = trie->root;
            return {};
        }
        else{
            currInput += c;
            if(node->words.find(c) == node->words.end()){
                node->words[c] = new Node();
            }
            node = node->words[c];
            vector<pair<int,string>> results;
            trie->search(node, results);
            sort(results.begin(), results.end());
            for(int i = 0; i < min((int)results.size(),3); ++i){
                res.push_back(results[i].second);
            }
            return res;
        }
    }
private:
    Node* node;
    Trie* trie;
    string currInput;
};

字符串的编码与解码

请你设计一个算法，可以将一个字符串列表编码成为一个字符串。这个编码后的字符串是可以通过网络进行高效传送的，并且可以在接收端被解码回原来的字符串列表。

1 号机（发送方）有如下函数：

string encode(vector<string> strs) {
  // ... your code
  return encoded_string;
}

2 号机（接收方）有如下函数：

vector<string> decode(string s) {
  //... your code
  return strs;
}

1 号机（发送方）执行： string encoded_string = encode(strs);

2 号机（接收方）执行： vector<string> strs2 = decode(encoded_string); 此时，2 号机（接收方）的 strs2 需要和 1 号机（发送方）的 strs 相同。

请你来实现这个 encode 和 decode 方法。注意：

因为字符串可能会包含 256 个合法 ascii字符中的任何字符，所以您的算法必须要能够处理任何可能会出现的字符。
请勿使用 “类成员”、“全局变量” 或 “静态变量” 来存储这些状态，您的编码和解码算法应该是非状态依赖的。
请不要依赖任何方法库，例如 eval 又或者是 serialize 之类的方法。

class Codec:
    def len_to_str(self, x):
        x = len(x)
        bytes = [chr(x >> (i * 8) & 0xff) for i in range(4)]
        bytes.reverse()
        bytes_str = ''.join(bytes)
        return bytes_str
    
    def encode(self, strs):
        # encode here is a workaround to fix BE CodecDriver error
        return ''.join(self.len_to_str(x) + x.encode('utf-8') for x in strs)
        
    def str_to_int(self, bytes_str):
        result = 0
        for ch in bytes_str:
            result = result * 256 + ord(ch)
        return result
    
    def decode(self, s):
        i, n = 0, len(s)
        output = []
        while i < n:
            length = self.str_to_int(s[i: i + 4])
            i += 4
            output.append(s[i: i + length])
            i += length
        return output

粉碎糖果

给定一个 m x n 的二维整数数组 board 代表糖果所在的方格，不同的正整数 board[i][j] 代表不同种

给定的方格是玩家移动后的游戏状态，现在需要你根据以下规则粉碎糖果，使得整个方格处于稳定状态并最终输出：

如果有三个及以上水平或者垂直相连的同种糖果，同一时间将它们粉碎，即将这些位置变成空的。
在同时粉碎掉这些糖果之后，如果有一个空的位置上方还有糖果，那么上方的糖果就会下落直到碰到下方的糖果或者底部，这些糖果都是同时下落，也不会有新的糖果从顶部出现并落下来。
通过前两步的操作，可能又会出现可以粉碎的糖果，请继续重复前面的操作。
当不存在可以粉碎的糖果，也就是状态稳定之后，请输出最终的状态。

你需要模拟上述规则并使整个方格达到稳定状态，并输出。

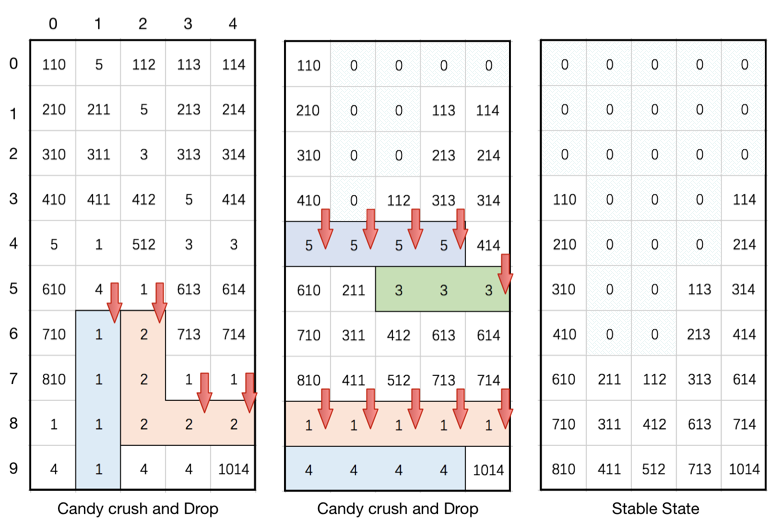
题解

分两部分：

粉碎糖果: 采用标记方法，如果连续3行或3列相同，将其标记为 -abs(v)，最后统一处理。
掉落糖果：我们可以使用滑动窗口方法，read 指针读元素，write 指针写元素。指针以逆序遍历列元素，当 read 指针遇到糖果时，write 指针将它写下来并移动到下一个位置。然后，write 指针将向列的其余部分写入零。

class Solution {
public:
    vector<vector<int>> candyCrush(vector<vector<int>>& g) {
        int n = g.size(), m = g[0].size();
        bool flag = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j + 2 < m; ++j) {
                int v = abs(g[i][j]);
                if (v && v == abs(g[i][j+1]) && v == abs(g[i][j+2])){
                    g[i][j]=g[i][j+1]=g[i][j+2]=-v;
                    flag = 1;
                }
            } 
        }
        for (int i = 0; i + 2 < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int v = abs(g[i][j]);
                if (v && v == abs(g[i+1][j]) && v == abs(g[i+2][j])) {
                    g[i][j]=g[i+1][j]=g[i+2][j]=-v;
                    flag = 1;
                }
            }
        }

        for (int j = 0; j < m; ++j) {
            int w = n - 1;
            for (int i = n - 1; ~i; --i) 
                if (g[i][j] > 0) g[w--][j] = g[i][j];
            while (w >= 0) g[w--][j] = 0;
        }
        return flag ? candyCrush(g) : g;
    }
};

最小窗口子序列

给定字符串 S and T，找出 S 中最短的（连续）子串 W ，使得 T 是 W 的子序列。

如果 S 中没有窗口可以包含 T 中的所有字符，返回空字符串 ““。如果有不止一个最短长度的窗口，返回开始位置最靠左的那个。

1.滑动窗口

    string minWindow(string s, string t) {
        int n = s.size(), m = t.size(), l = 0, r = n -1;
        if (n == m && s == t) return s;
        int p1 = 0, p2 = 0;
        while (p1 < n) {
            if (s[p1] == t[p2]) ++p2;
            if (p2 == m) {
                int rt = p1;
                --p2;
                while (p2 >= 0) {
                    if (s[p1] == t[p2]) --p2;
                    --p1;
                }
                ++p1;
                if (rt - p1 < r - l) {
                    l = p1, r = rt;
                }
                p2 = 0;
            }
            ++p1;
        }
        return r - l + 1 == n ? "": s.substr(l, r - l + 1);
    }

中缀表达式求值

实现一个基本的计算器来计算简单的表达式字符串。

表达式字符串只包含非负整数，算符 +、-、*、/ ，左括号 ( 和右括号 ) 。整数除法需要向下截断。你可以假定给定的表达式总是有效的。所有的中间结果的范围为int范围内。

示例：

输入：s = "2*(5+5*2)/3+(6/2+8)"
输出：21

class Solution {
public:
    stack<int> num, op;
    map<char, int> m;
    void eval() {
        int b = num.top(); num.pop();
        int a = num.top(); num.pop();
        int opr = op.top(); op.pop();
        int x;
        if (opr == '+') x = a + b;
        else if (opr == '-') x = a - b;
        else if (opr == '*') x = a * b;
        else x = a / b;
        num.push(x);
    }
    int calculate(string s) {
        m['+'] = m['-'] = 1;
        m['*'] = m['/'] = 2;
        for (int i = 0; i < s.size(); ++i) {
            if (isdigit(s[i])) {
                int j = i + 1, tmp = s[i] - '0';
                while (j < s.size() && isdigit(s[j])) {
                    tmp = tmp * 10 + s[j] - '0';
                    j++;
                }
                num.push(tmp);
                i = j - 1;
            } else if (s[i] == '(') {
                op.push(s[i]);
            } else if (s[i] == ')') {
                while (op.top() != '(') eval();
                op.pop();
            } else {
                while (op.size() && m[op.top()] >= m[s[i]]) {
                    eval();
                }
                op.push(s[i]);
            }
        }
        while (op.size()) eval();
        return num.top();
    }
};

字符串转化

给出两个长度相同的字符串，分别是 str1 和 str2。请你帮忙判断字符串 str1 能不能在零次或多次转化后变成字符串 str2。

每一次转化时，将会一次性将 str1 中出现的所有相同字母变成其他任何小写英文字母（见示例）。

只有在字符串 str1 能够通过上述方式顺利转化为字符串 str2 时才能返回 True，否则返回 False。

分析

1. s1中两个下标 i,j 值相同时，s2中对应下标也必须相同
1. 为了转换过程不影响后续转换，需要找一个s2中存在的字符做过渡，如果s2中出现26个不同字母，则不能进行转换

class Solution:
    def canConvert(self, s1: str, s2: str) -> bool:
        if s1 == s2:
            return True
        m = dict()
        vis = set()
        for i in range(len(s1)):
            if s1[i] not in m:
                m[s1[i]] = s2[i]
                vis.add(s2[i])
            elif m[s1[i]] != s2[i]:
                return False
        return len(vis) < 26

轰炸敌人

想象一下炸弹人游戏，在你面前有一个二维的网格来表示地图，网格中的格子分别被以下三种符号占据：

‘W’ 表示一堵墙
‘E’ 表示一个敌人
‘0’（数字 0）表示一个空位

请你计算一个炸弹最多能炸多少敌人。由于炸弹的威力不足以穿透墙体，炸弹只能炸到同一行和同一列没被墙体挡住的敌人。

注意：你只能把炸弹放在一个空的格子里

分析

递推，四个方向递推动态规划

    int maxKilledEnemies(vector<vector<char>>& grid) {
        int n = grid.size(), m = n ? grid[0].size() : 0, ans = 0;
        vector<vector<int>> dp(n, vector<int>(m, 0));

        for (int i = 0; i < n; ++i) {
            for (int j = 0, pre = 0; j < m; ++j) { 
                pre = grid[i][j] == 'W' ? 0 :(grid[i][j] == 'E' ? pre + 1 : pre);
                dp[i][j] += pre;
            }
            for (int j = m - 1, pre = 0; j >= 0; --j) {
                pre = grid[i][j] == 'W' ? 0 :(grid[i][j] == 'E' ? pre + 1 : pre);
                dp[i][j] += pre;
            }
        }
        for (int j = 0; j < m; ++j) {
            for (int i = 0, pre = 0; i < n; ++i) {
                pre = grid[i][j] == 'W' ? 0 :(grid[i][j] == 'E' ? pre + 1 : pre);
                dp[i][j] += pre;
            }
            for (int i = n - 1, pre = 0;i >= 0; --i) {
                pre = grid[i][j] == 'W' ? 0 :(grid[i][j] == 'E' ? pre + 1 : pre);
                dp[i][j] += pre;
            }
        }
        for (int i = 0; i < n; ++i) 
            for (int j = 0; j < m; ++j)
                if (grid[i][j] == '0')
                    ans = max(ans, dp[i][j]);
        return ans;
    }

离建筑物最近的距离

你是个房地产开发商，想要选择一片空地建一栋大楼。你想把这栋大楼够造在一个距离周边设施都比较方便的地方，通过调研，你希望从它出发能在最短的距离和内抵达周边全部的建筑物。请你计算出这个最佳的选址到周边全部建筑物的最短距离和。

提示：

你只能通过向上、下、左、右四个方向上移动。
给你一个由 0、1 和 2 组成的二维网格，其中：
- 0 代表你可以自由通过和选择建造的空地
- 1 代表你无法通行的建筑物
- 2 代表你无法通行的障碍物

分析多次bfs

int go[4][2] = {1,0,-1,0,0,1,0,-1};
int shortestDistance(vector<vector<int>>& g) {
    int n = g.size(), m = g[0].size(), cnt = 0, res;
    vector<vector<int>> dis(n, vector<int>(m)), sum = dis;
    queue<pair<int, int>> q;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (g[i][j] == 1) {
                res = INT_MAX;
                q.push({i, j});
                while (!q.empty()) {
                    int x = q.front().first, y = q.front().second;
                    q.pop();
                    for (int k = 0; k < 4; ++k) {
                        int nx = x + go[k][0], ny = y + go[k][1];
                        if (nx>=0 && nx<n && ny>=0 && ny<m && g[nx][ny] == cnt) {
                            --g[nx][ny];
                            dis[nx][ny] = dis[x][y] + 1;
                            sum[nx][ny] += dis[nx][ny];
                            res = min(res, sum[nx][ny]);
                            q.push({nx, ny});
                        }
                    }
                }
                if (res == INT_MAX) return -1;
                --cnt;
            }
        }
    }
    return res;
}

分享巧克力

你有一大块巧克力，它由一些甜度不完全相同的小块组成。我们用数组 sweetness 来表示每一小块的甜度。你打算和 K 名朋友一起分享这块巧克力，所以你需要将切割 K 次才能得到 K+1 块，每一块都由一些连续的小块组成。

为了表现出你的慷慨，你将会吃掉总甜度最小的一块，并将其余几块分给你的朋友们。请找出一个最佳的切割策略，使得你所分得的巧克力总甜度最大，并返回这个最大总甜度。

    vector<int> nums;
    int sum, k;
    bool check(int sum, int x, int k) {
        int s = 0, cnt = 0;
        for (int i = 0; i < nums.size(); ++i) {
            s += nums[i];
            if (s >= x) {
                cnt++; s = 0;
            }
        }
        return cnt >= k + 1;
    }
    int maximizeSweetness(vector<int>& sweetness, int K) {
        nums = sweetness;
        sum = accumulate(nums.begin(), nums.end(), 0), k = K;
        int l = 0, r = sum / (k + 1);
        while (l < r) {
            int mid = l + (r - l + 1) / 2;
            if (check(sum, mid, k)) l = mid;
            else r = mid - 1;
        }
        return l;
    }

最小化去加油站的最大距离

整数数组 stations 表示水平数轴上各个加油站的位置。给你一个整数 k 。请你在数轴上增设 k 个加油站，新增加油站可以位于水平数轴上的任意位置，而不必放在整数位置上。

设 penalty() 是：增设 k 个新加油站后，相邻两个加油站间的最大距离。请你返回 penalty() 可能的最小值。与实际答案误差在 10-6 范围内的答案将被视作正确答案。

数据范围

10 <= stations.length <= 2000
0 <= stations[i] <= 1e8
stations 按严格递增顺序排列
1 <= k <= 1e6

二分法

定义 check(d)：有 k 个加油站，有没有可能让最小的最大距离小于等于d？这个问题的结果是单调的，因此可以用二分搜索来找到答案d,

    vector<int> nums;
    bool check(double d, int k) {
        int cnt = 0;
        for (int i = 0; i < nums.size() - 1; ++i) 
            cnt += (int)((nums[i + 1] - nums[i]) / d);
        return cnt <= k;
    }
    double minmaxGasDist(vector<int>& stations, int k) {
        nums = stations;
        double l = 0, r = 1e8;
        while (r - l > 2e-6) {
            double mi = (l + r) / 2.0;
            if (check(mi,k)) r = mi;
            else l = mi;
        }
        return l;
    }