记录算法题中能用到的数学公式和结论,遇到新的再补充。
===
Index
数论
- 给定两个正整数 n 和 m, n和m 互质, 求n和m的线性组合中,不能组合出的最大数字
n * m - n - m
- 一个数各位数字之和能被 3 整除,则这个数能被3整除,一个数各位数字之和能被 9 整除,则这个数能被9整除。
- 如果一个整数的奇数位数字之和与偶位数数字之和之差能被11整除,那么这个数能被11整除。
- 如果一个数末三位与末三位以前的数字合成数之差能被7,11,或13整除,那么这个数能被7,11或13整除。
- 求一组分数的最大公约数
- 求出各个分数分母的最小公倍数a,各个分子的最大公约数b,则
b/a即为所求。
- 求出各个分数分母的最小公倍数a,各个分子的最大公约数b,则
- 求一组分数的最小公倍数
- 求出各个分数分母的最大公约数a,各个分子的最小公倍数b,则
b/a即为所求。
- 求出各个分数分母的最大公约数a,各个分子的最小公倍数b,则
- x^y 与 x + y 的奇偶性改变原则相同
- 对于一个单增序列,所有的 pair 中 Xor 的最小值出现在相邻两个数之间
- Prime Gap: 10^18次方以内的数,相邻两个素数之间的间距不超过1500.
- 曼哈顿距离
|x1-x2|+|y1-y2|=max( |(x1+y1)-(x2+y2)|, |(x1-y1)-(x2-y2)| ),配合数据结构,可以快速求出曼哈顿距离最远的点。 - 如果 a+b=c, 求满足 gcd(a,b)=1 的 (a,b) 的个数, 等价于求 gcd(c,a)=1 或者 gcd(c,b)=1 的个数。即欧拉函数。
- 有2n个不同的小球,需要两两配对成 n 对,问最终有多少种方案。
(2*n)!/(2!n!)用n!给 n 对松绑,然后用2!给每对之间的顺序松绑。
- 有 n 个相同且连续的空位, k 个相同的砖块,每块砖会占用连续的 m 个空位。问这 k 块砖有多少种放法。
C(n-k(m-1), k), 先把需要额外占的位置从 n 里面取出来,然后再当成 m=1 算
排列组合
-
定义一个非负整数是不降数,当且仅当它的各位数字从高位到低位单调不降。 例如,1111, 1234都是不降数,请你求出恰好n位的不降数的个数。
数据范围:
1 <= n <= 1e8
答案:
考虑先算低于 n 位的数字有多少。我们把数字看成长为 n 的序列,然后统计差分序列的数量即可。考虑枚举差分序列之和 i,然后通过插板法,可以得到答案是:
答案: combi(n + 8, 8)
蚂蚁掉落问题
n只蚂蚁以每秒1的速度在长为L的竿子上爬行,蚂蚁爬到竿子的端点时会掉落,两只蚂蚁相遇时,立即各自往相反方向爬回去。
问题1
对于每只蚂蚁,我们知道它距离竿子左端的距离xi,但不知道它当前的朝向。请计算所有蚂蚁落下竿子所需的最短时间和最长时间。
分析 当两只蚂蚁相遇后,可以认为它们保持原样交错而过继续前进,也就是认为每只蚂蚁时独立运动的,所以最长时间即为所有蚂蚁距离两端的最长距离。
最短时间同理。
vector<int> minMaxDropTime(vector<int> &p, int L) {
int mint = 0, maxt = 0;
for (int i = 0; i < n; ++i) {
mint = max(mint, min(p[i], L - p[i]));
maxt = max(maxt, max(p[i], L - p[i]));
}
return {mint, maxt};
}
问题2
设第i个蚂蚁的编号为i,给定每个蚂蚁的位置和前进方向,求每个蚂蚁的掉落时间。
结论
- 设整条木根上有n只蚂蚁,有x只向左,y只向右,根据设定,蚂蚁相遇会改变方向,但因速度相同,两者的相对位置不回发生改变。 即所有蚂蚁的相对位置永远不变
- 经过无限之间后,结果一定是x只从左边掉落,y只从右边掉落
- 对于蚂蚁a
- 如果其左边蚂蚁数量小于向左走的蚂蚁数量,蚂蚁a (初始状态从左到右相对位置为k)的掉落时间等于初始状态下向左走的第k只蚂蚁在不发生相遇情况下的掉落时间。
- 否则,蚂蚁a(从右向左相对位置为k’=n-k+1)的掉落时间等于初始状态下向右走的第k只蚂蚁在不发生相遇情况下的掉落时间。
也就是说,我们认为两蚂蚁相遇交换的不只是速度,而是使命(向着初始方向到达端点),我们可以认为初始状态下某只蚂蚁的使命一直在执行,只不过途中可能会交给另一只蚂蚁去执行。 在情况1下,蚂蚁a的最终形式的时初始状态下向左走的第k只蚂蚁的使命。
/*
ants[i] = [pi, di] pi是第i只蚂蚁的位置,di是方向,0表示向左走,1表示向右走
返回ans:ans[i]是第i只蚂蚁掉落的时间
*/
vector<int> antDropTime(vector<vector<int>> &ants, int L) {
int n = ants.size(), l = 0, r = n - 1;
vector<int> ans(n);
vector<pair<int,int>> p;
vector<array<int,3>> a;
for (int i = 0; i < n; ++i) {
a.push_back({ants[i][0], ants[i][1], i});
if (ants[i][1] == 0) p.push_back({ants[i][0], 0});
else p.push_back({L - ants[i][0], 1});
}
sort(p.begin(), p.end());
sort(a.begin(), a.end(), [&](auto x, auto y){return x[0] < y[0];});
for (auto &[x, y]: p) {
if (y == 0) ans[a[l++][2]] = x;
else ans[a[r--][2]] = x;
}
return ans;
}
问题3
求每只蚂蚁的掉落方向或顺序。
- 方向:设有x只向左,y只向右,则相对位置前x只向左掉落,后y只向右掉落。
- 顺序:求出掉落时间,按照掉落时间排序即可。
相关题目
区间中异或值最大的两个数
给定一个区间[a,b],在区间里寻找两个数x和y,使得x异或y最大
- a < b < 2e63
结论
结果都是 2^n - 1,需要求一下n的大小。
long long maxXorSum(long long a, long long b) {
long long x = a ^ b, cnt = 1;
while (x) {
cnt++;
x >>= 1;
}
return (1LL) << cnt - 1;
}
部分结论题
- n个人一圈做一个游戏,从第一个人开始,每隔一个人移除一个人,问第k个移除的人是谁?
- 1 <= k <= n <= 1e9
int kth_del(int n, int k) {
if (n == 1) return 1;
if (k <= (n + 1) / 2)
return 2 * k > n ? 2 * k % n : 2 * k;
int c = kth_del(n >> 1, k - (n + 1) / 2);
return n & 1 ? 2 * c + 1 : 2 * c - 1;
}
括号序列
下一个平衡括号序列
| 给出平衡的括号序列 s,我们要求出按字典序升序排序的长度为 | s | 的所有平衡括号序列中,序列 s 的下一个平衡括号序列。在本问题中,我们认为左括号的字典序小于右括号,且不考虑变种括号序列。 |
时间复杂度 O(n)
bool next_balanced_sequence(string &s) {
int n = s.size(), dep = 0;
for (int i = n - 1; i >= 0; --i) {
dep += (s[i] == '(') ? -1 : 1;
if (s[i] == '(' && dep > 0) {
dep--;
int l = (n - i - 1 - dep) / 2, r = n - i - 1 - l;
string t = s.substr(0, i) + ')' + string(l, '(') + string(r, ')');
s.swap(t);
return true;
}
}
return false;
}
括号序列的字典序排名
给出平衡的括号序列 s,我们要求出它的字典序排名。
时间复杂度 O(n*n) 排名从1开始
using T = long long; //mint
T rank_of_sequence(string &s) {
int n = s.size();
vector dp(n + 1, vector<T>(n + 1));
dp[0][0] = 1;
for (int i = 1; i < n; ++i) {
dp[i][0] = dp[i - 1][1];
for (int j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
}
}
int idx = 0;
T ans = 0;
for (int i = 1; i <= n; ++i) {
if (s[i - 1] == ')') ans += dp[n - i][idx + 1], idx--;
else idx++;
}
return ans + 1;
}
第k个平衡括号序列
在所有包含n对括号的平衡括号序列中,求字典序第k小的括号序列。
using T = long long;
string kth_balanced(int n, T k) { // n对括号,字符串长度为2*n
vector d(2 * n + 1,vector<T>(n + 1));
d[0][0] = 1;
for (int i = 1; i <= 2 * n; ++i) {
d[i][0] = d[i - 1][1];
for (int j = 1; j < n; ++j)
d[i][j] = d[i-1][j-1] + d[i-1][j+1];
d[i][n] = d[i-1][n-1];
}
string ans;
int dep = 0;
for (int i = 0; i < 2 * n; ++i) {
if (dep + 1 <= n && d[2 * n - i - 1][dep + 1] >= k) {
ans += '(';
dep++;
} else {
ans += ')';
if (dep + 1 <= n) k -= d[2 * n - i - 1][dep + 1];
dep--;
}
}
return ans;
}
平衡括号子串数目
一个只包含’(‘和’)’的字符串S, 求有多少个非空子串是平衡括号序列
- 1 <= s.size() <= 1e6
分析
对于平衡的括号序列,右括号 一定只能和一个左括号 匹配。
我们可以跑一遍栈,得到右括号匹配的左括号。
其中 pos[i] 保存着匹配的左括号的下标。
可以定义 dp[i] 为,s[i] 为右括号作为结尾的情况下,平衡子串的个数。
我们知道 [pos[i], i] 是一个平衡子串的,我们需要看看 dp[pos[i] - 1] 的值。
所以 dp[i] = dp[pos[i] - 1] + 1。
时间复杂度 O(n)
long long countValidSeq(string &s) {
int n = s.size();
vector<int> pos(n + 1);
stack<int> sk;
for (int i = 1; i <= n; ++i) {
if (s[i - 1] == '(') sk.push(i);
else {
if(sk.size()) {
pos[i] = sk.top();
sk.pop();
}
}
}
long long ans = 0;
vector<long long> dp(n + 1);
for (int i = 1; i <= n; ++i) {
if (pos[i]) {
dp[i] = dp[pos[i] - 1] + 1;
ans += dp[i];
}
}
return ans;
}
获得平衡括号串的最少交换次数
长度为2n的字符串,包含n个’(‘和n个’)’,每次操作可以交换相邻的两个字符,求将字符串变为平衡括号串的最少交换次数。
时间复杂度 O(n)
long long minSwapCount(string &s) {
int n = s.size(), cnt = 0;
long long ans = 0;
for (int i = 0; i < n; ++i) {
if (s[i] == '(') {
cnt++;
} else cnt--;
if (cnt < 0) ans ++, cnt += 2;
}
return ans;
}
数列
等差与等比数列
等差数列
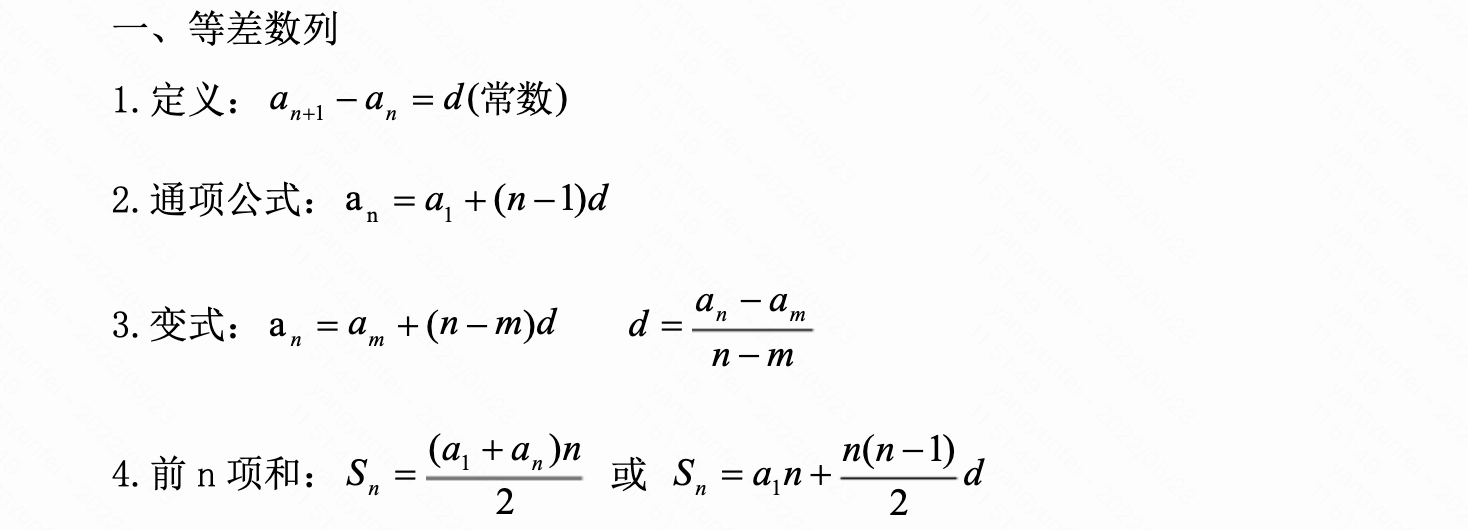

等差数列前n项和
long long arith_seq_sum(long long a1, long long d, long long n) {
return a1 * n + n * (n - 1) * d / 2;
}
等比数列
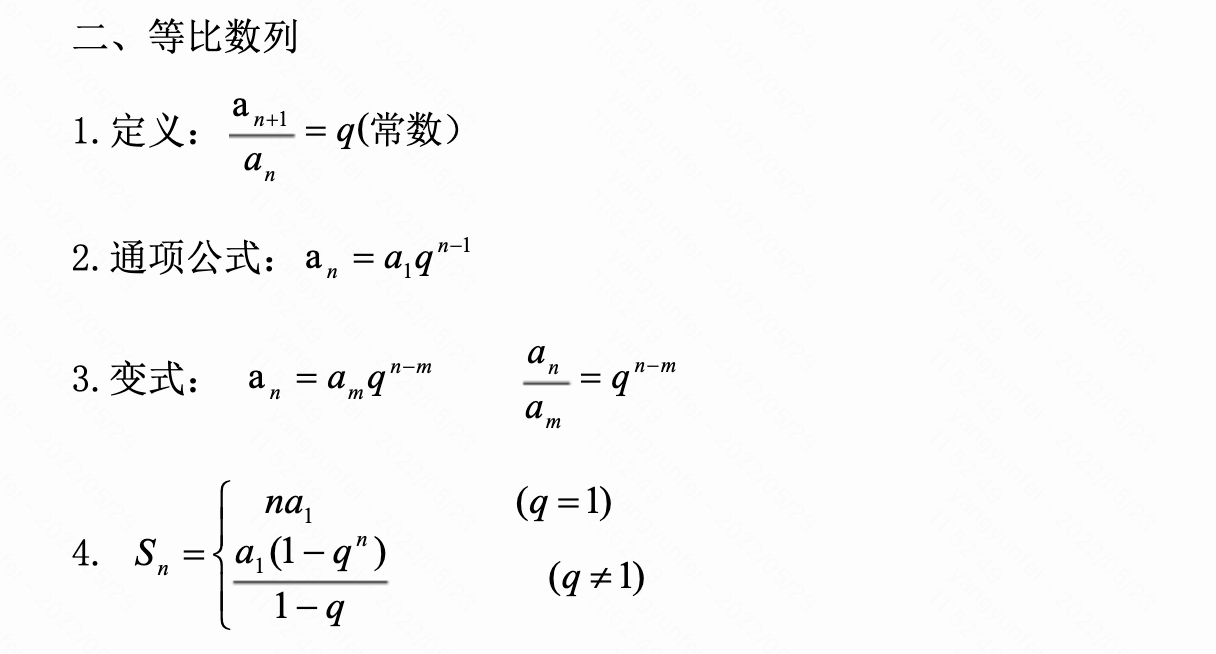

等比数列前n项和
mint geo_seq_sum(mint a1, mint q, int n) {
if (q == 1) return a1 * n;
return a1 * (q.pow(n) - 1) / (q - 1);
}
等比数列前n项和取模
给定整数 a, x, m, 求 (1+a+a^2+...+a^(x-1) mod m 的和。
- 1 <= a, m <= 1e9
- 1 <= x <= 1e12
注意
直接使用前n项和公式需要求 a-1的逆元,但是 a-1 模m的逆元可能不存在,所以可以使用分治的算法。
long long qpow(long long m, long long k, long long p) {
long long res = 1 % p, t = m;
while (k) {
if (k&1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return (long long)res;
}
long long calc(long long p, long long c, int mod) {
if (c == 0) return 1;
long long x;
if (c % 2 == 0)
x = (1 + qpow(p, c / 2, mod)) * calc(p, c/2 - 1, mod) + qpow(p, c, mod);
else
x = (1 + qpow(p, (c + 1)/ 2, mod)) * calc(p, (c - 1) / 2, mod);
x %= mod;
return x;
}
long long sum_mod(long long a, long long x, long long mod) {
if (a == 1) return x % mod;
if (mod == 1) return 0;
return calc(a, x - 1, mod);
}
常见数列前n项和公式

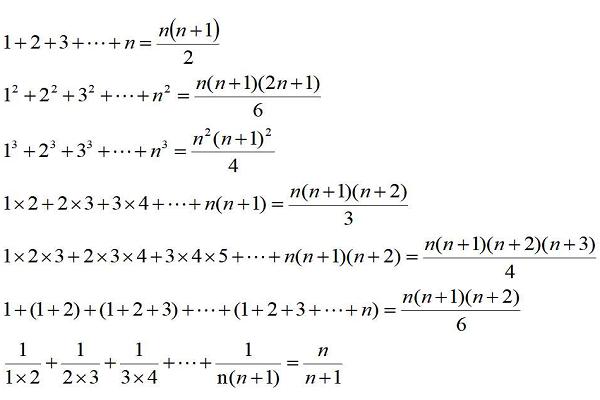
第一类stirling数
第一类斯特林数表示表示将 n 个不同元素构成m个圆排列的数目.
第一类斯特林数 把N个不同元素分为k个环,每个环非空,问有多少分法,记为S(p,k) S(p,p) = 1, S(p,0) = 0
递推公式: S(p,k) = (p - 1) * S(p-1, k) + s(p - 1, k - 1)
p个人排k个圈,一种方法是,第k个圈只有p自己, 其数目为 s(p-1, k-1). 还有一种方法是
p加入p-1人组成得k个圈,排在任意一个人的左边,其数目为 (p-1)*S(p-1,k) .
实例
- 设f(i,j)表示i个数的排列,存在j个数,在它们前面没有比他们大的数。考虑最小的数放在哪,可以得到递推式:
f(i,j)=f(i-1,j-1)+(i-1)*f(i-1,j)。
例题
class Solution {
public:
using ll = long long;
const ll mod = 1e9 + 7;
int rearrangeSticks(int n, int k) {
vector<vector<ll>> f(n + 1, vector<ll>(n + 1));
f[1][1] = 1;
for (int i = 2; i <= n; ++i)
for (int k = 1; k <= i; ++k)
f[i][k] = (f[i-1][k]*(i-1) + f[i-1][k-1]) % mod;
return f[n][k];
}
};
第二类stirling数
s(n,k)表示含n个元素的集合划分为k个集合的情况数。
递推公式: s(n,k)=s(n-1,k-1)+k·s(n-1,k),1≤k<n
卡塔兰(catalan)数列
实例:
- 有 2n 个人排成一行进入剧场。入场费 5 元。其中只有 n 个人有一张 5 元钞票,另外 n 人只有 10 元钞票,剧院无其它钞票,问有多少中方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?
- 一位大城市的律师在她住所以北 n 个街区和以东 n 个街区处工作。每天她走 2n 个街区去上班。如 果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
- 在圆上选择 2n 个点,将这些点成对连接起来使得所得到的 n 条线段不相交的方法数?
- n 个结点可构造多少个不同的二叉树?
- 一个栈(无穷大)的进栈序列为 1,2,3,…n,有多少个不同的出栈序列?
- 将一个凸多边形区域分成三角形区域的方法数?
- 一个乘法算式 P=a1a2a3…an,在保证表达式合法的前提下(某个数不会被括号括两次,如“((a))” 是错误的),有多少种添加括号的方法?
通项公式 : a_n = C(2n, n) / (n + 1)
递推公式: a_1 = 1, a_n = 2(2n-1) / (n+1) , n >= 2
分平面的最大区域数
-
n条直线分平面的最大区域数的序列为:2,4,7,11,… 递推公式:f_n=f_{n-1}+n 通项公式:f_n=n(n+1)/2+1
-
n条折线分平面的最大区域数的序列为:2,7,16,29,… 递推公式:
f_n=f_{n-1}+4n-3通项公式:f_n=(n-1)(2n-1)+2n -
n条封闭曲线(如一般位置上的圆)分平面的最大区域数的序列为:2,4,8,14,… 递推公式:
f_n=f_{n-1}+2(n-1)通项公式:f_n=n^2-n+2





