数学/数论算法

2020-09-04 | 阅读：次

===

Index

大数取模
快速幂运算
64位数乘法
最大公约数
最小公倍数
试除法判定质数
试除法分解质因数
素数筛法
欧拉函数
扩展欧几里得算法
高斯消元
组合计数
前缀和
约瑟夫环
卡特兰数
施罗德数
NIM游戏

大数取模

取模运算的性质：

因为 (a%n) - (b%n) 可能小于 n，所以 +n

因为 (a%n)(b%n) 可能溢出，计算前应该强转为 long long

a * b % m = (a % m) * (b % m) % m

输入 a 为长度小于 1000 的字符串，b 为小于 100000 的整数

    int big_mod(const string& a, int b) {
        long long ret = 0;
        for (auto c : a) {
            ret = ((ret * 10) % b + (c - '0') % b) % b;
        }
        return (int)ret;
    }

快速幂运算

计算 a^n % mod

时间复杂度：O(log(n))

    int qmi(int a, int n, int mod) {
        long long res = 1;
        while (n) {
            if (n & 1)
                res = res * a % mod;
            a = (long long)(a * a) % p;
            n >>= 1;
        }
        return (int)res;
    }

64位数乘法

ll mul(ll a, ll b, ll p) {
    ll ans = 0;
    for (; b; b >>= 1) {
        if (b & 1) ans = (ans + a) % p;
        a = (ll) a * 2 % p;
    }
    return ans;
}

最大公约数

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

最小公倍数

int lcm(int a, int b) {
    return a / gcd(a, b) * b;
}

试除法判定质数

bool isPrime(int x) {
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

试除法分解质因数

vector<pair<int,int>> getDivisors(int x) {
    vector<pair<int,int>> res;
    for (int i = 2; i <= x / i; ++i) {
        if (x % i == 0) {
            int s = 0;
            while (x % i == 0) 
                x /= i, s++;
            res.emplace_back(i,s);
        }
    }
    if (x > 1) res.emplace_back(x,1);
    return res;
}

试除法求所有约数

vector<int> getDivisors(int x) {
    vector<int> res;
    for (int i = 1; i <= x / i; ++i) 
        if (x % i == 0) {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    sort(res.begin(), res.end());
    return res;
}

素数筛法

1.朴素筛法求素数

时间复杂度 O(nlog(n))

int primes[N], cnt; // primes[]存储所有素数
bool st[N];   //st[x]存储x是否被筛掉
void getPrimes(int n) {
    for (int i = 2; i <= n; ++i) {
        if (st[i]) continue;    //st[i]说明i不是素数
        primes[cnt++] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

2.埃氏筛素数

时间复杂度：O(nloglogn)

int primes[N], cnt; // primes[]存储所有素数
bool st[N];   //st[x]存储x是否被筛掉
void getPrimes(int n) {
    for (int i = 2; i <= n; ++i) {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = 2 * i; j <= n; j += i)
            st[j] = true;
    }
}

3.线性筛法求素数

时间复杂度 O(n)

n只会被最小的质因子筛掉，每个数只有一个最小质因子，所以每个数只会被筛一次

当pj∣i时，pj一定是i的最小质因子，也一定是pj∗i的最小质因子

当pj∤i时，pj一定小于i的最小质因子，pj也一定是pj∗i的最小质因子

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];
void getPrimes(int n) {
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) 
            primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; ++j) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) 
                break;
        }
    }
}

约数个数和约数之和

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

欧拉函数

定义：1 ~ N中 与 N 互质的数的个数被称为欧拉函数，记为ϕ(N)
若 N = p1^a1 * p2^a2 * ... * pm^am 则：
ϕ(N) = N * (p1-1)/p1 * (p2-1)/p2 * ... * (pm-1)/pm

    int phi(int x) {
        int res = x;
        for (int i = 2; i <= x / i; i ++ )
            if (x % i == 0) {
                res = res / i * (i - 1);
                while (x % i == 0) x /= i;
            }
        if (x > 1) res = res / x * (x - 1);
        return res;
    }

筛法求欧拉函数（求1 ~ n中每个数的欧拉函数之和是多少）

借鉴线性筛法的思路

当i为质数时，ϕ(i)=i−1

枚举质数过程中：

当pj∣i时，pj一定是i的最小质因子，则

ϕ(pj*i) = pj * ϕ(i)

当pj∤i时，pj一定小于i的最小质因子，pj也一定是pj∗i的最小质因子, 则

ϕ(pj*i) = (pj - 1) * ϕ(i)

int primes[N], cnt;     // primes[]存储所有素数
int euler[N];           // 存储每个数的欧拉函数
bool st[N];         // st[x]存储x是否被筛掉

void get_eulers(int n) {
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ ) {
        if (!st[i]) {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ ) {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0) {
                euler[t] = euler[i] * primes[j];
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}

扩展欧几里得算法

求x, y，使得ax + by = gcd(a, b)

    int exgcd(int a, int b, int &x, int &y) {
        if (!b) {
            x = 1; y = 0;
            return a;
        }
        int d = exgcd(b, a % b, y, x);
        y -= (a/b) * x;
        return d;
    }

高斯消元

m 个方程，n个未知数的线性方程组

a11 * x1 + ... + a1n * xn = b1
a21 * x1 + ... + a2n * xn = b2
...
an1 * x1 + ... + ann * xn = bn

初等行变换：把某一行乘一个非零的数，交换某两行，把某行的若干倍加到另一行 解的个数：根据最后得到的上三角矩阵判断

如果是完美的阶梯型矩阵，则有唯一解；

如果存在0=b(b≠0)的行，则无解；

否则有无穷解（存在0=0的行）

步骤：

枚举每一列c：

找到当前这一列绝对值最大的一行；

将该行换到未固定的方程的最上方，之后将该方程固定；

将该行第一个非零数变成1；

将下方所有行的第c列消成0

   // a[N][N]是增广矩阵
    int gauss() {
        int c, r;

        for (c = 0, r = 0; c < n; c++) {
            int t = c;

            for (int i = r; i < n; i++)
                if (abs(a[i][c]) > abs(a[t][c]))
                    t = i;

            if (abs(a[t][c]) < eps) continue;

            for (int i = c; i < n + 1; i++) swap(a[t][i], a[r][i]);
            for (int i = n; i >= 0; i--) a[r][i] /= a[r][c];

            for (int i = r + 1; i < n; i++)
                if (abs(a[i][c]) > eps)
                    for (int j = n; j >= c; j--)
                        a[i][j] -= a[r][j] * a[i][c];

            r++;
        }

        if (r < n) {
            for (int i = r; i < n; i++)
                if (abs(a[i][n]) > eps)
                    return 0;

            return 1;
        }

        for (int i = n - 1; i >= 0; i--)
            for (int j = i + 1; j < n; j++)
                a[i][n] -= a[j][n] * a[i][j];

        return 2;
    }

组合计数

数据不同范围，对时间复杂度要求不同

求 c(a, b) mod (1e9 + 7)

1 <= b <= a <= 2000

时间复杂度 O(n^2)

    for (int i = 0; i < N; i ++ )
        for (int j = 0; j <= i; j ++ )
            if (!j) c[i][j] = 1;
            else 
                c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

求 c(a, b) mod (1e9 + 7)

1 <= b <= a <= 10^5

时间复杂度 O(n(log(n)))

预处理出所有数的阶乘和逆元，mod是质数，可以用费马小定理

    void init() {
        fact[0] = infact[0] = 1;
        for (int i = 1; i < N; i ++ ) {
            fact[i] = fact[i - 1] * i % mod;
            infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
        }
    }

求 c(a, b) mod p

1 <= b <= a <= 10^18, 1 <= p <= 10^5, p 是质数

O(p * log(p) * log_p(N))

Lucas定理:c(a,b) ≡ c(a mod p, b mod p) * c(a/p, b/p) (mod p)

using LL = long long;
LL C(int a, int b) {
    LL ret = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- ) {
        ret = ret * j % p;
        ret = ret * qmi(i, p - 2) % p;
    }
    return ret;
}

LL lucas(LL a, LL b) {
    if (a < p && b < p) return C(a, b);
    return C(a % p, b % p) * lucas(a / p, b / p) % p;
}

前缀和

一维前缀和

 for(int i = 1;i <= n; i++) 
    s[i] = s[i - 1] + a[i];

二维前缀和

for (int i = 1; i <= n; ++i) 
    for (int j = 1; j <= m; ++j) 
        s[i][j] = s[i- 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i - 1][j - 1];

约瑟夫环

0,1,...n-1 这n个数排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字，求出这个圆圈里剩下的最后一个数字。

一句话题解：通过剩余x人时的答案，反推x+1人时的答案。由于只剩一个人时答案必然为0，层层反推即可。首先，我们用f(n)表示剩下n个人的时候，从当前起点开始走f(n)步会到达赢家的位置。假设现在有n个人活着，那么当前起点是0，，杀完编号为m-1的人后，新的起点则是m，假设f(n - 1)已知，那么我们需要走m步到新的起点，再走f(n-1)步走到赢家的位置，即一共需要走的步数为： m + f(n - 1) // m是新起点，f(n-1)是额外步数

int lastRemaining(int n, int m) {
    /*
    设idx表示上一次的结果，l表示当前人数，
    则 f(l) = (m + idx) % l;
    */
    int idx = 0;
    for (int l = 2; l <= n; ++l) {
        idx = (m + idx) % l;
    }
    return idx;
}

卡特兰数

给定n个0和n个1，它们按照某种顺序排成长度为2n的序列.
满足任意前缀中0的个数都不少于1的个数的序列的数量为： 
Cat(n) = C(2n, n) / (n + 1)

施罗德数

在组合数学中，施罗德数用来描述从 (0,0)(0,0) 到 (n,n)(n,n) 的网格中，只能使用 (1,0)、(0,1)、(1,1)(1,0)、(0,1)、(1,1) 三种移动方式，始终位于对角线下方且不越过对角线的路径数。

施罗德数的前几项(从第 00 项算起)为 1,2,6,22,90,394,1806,8558,41586,2060981,2,6,22,90,394,1806,8558,41586,206098…… 下图为 n=1,2,3n=1,2,3 时的施罗德路径

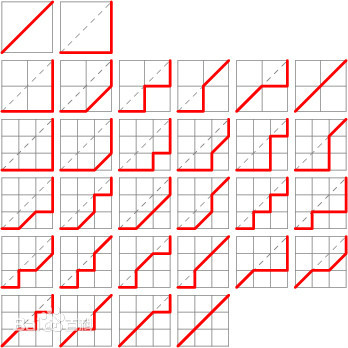
施罗德数的递推公式为: s_i = s_(i-1) + sigma(j = 0, i - 1) s_j * s _ (n-j-1)

不过 O(n2)的递推在 1e5级别的数据面前显然是要超时的

有递推式 (i + 1)F_i = (6n - 3)F_(i-1) - (i - 2)F_(i - 2)

使得 F_0 = S_0, 对于任意的 i >= 1 ,都有 2*F_i = S_i

using LL = long long;
const int N = 100010, mod = 1e9 + 7;

int qmi(int a, int k) {...}

LL f[N], s[N];

void init(int n) {
    f[0] = s[0] = f[1] = 1;
    s[1] = 2;
    for (int i = 2; i <= n; ++i) {
        f[i] =  ((6*i-3) * f[i-1] - (i-2) * f[i-2]) % mod * qmi(i+1, mod-2) % mod;
        s[i] = f[i] * 2 % mod;
    }
}

nim游戏

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。

所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。 NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理：NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ … ^ An != 0

king-yyf