===
Index
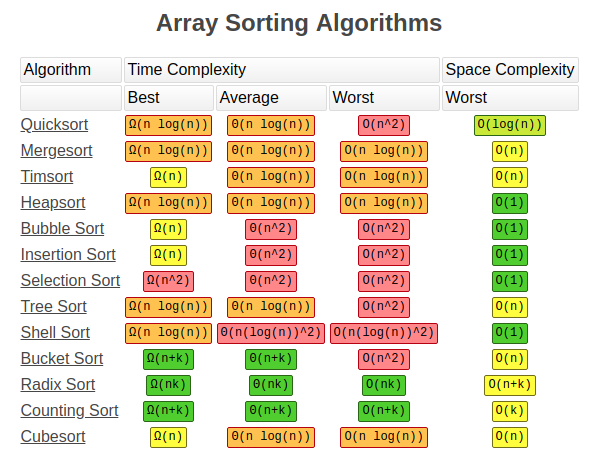
总结几种常用排序算法。 原理部分参考自:https://www.jianshu.com/p/916b15eae350。
插入排序
思路是类似扑克牌的排序,每次从未排序序列的第一个元素,插入到已排序序列中的合适位置。假设初始的有序序列为第0个元素(本文描述的序号都从0开始),只有一个元素的序列肯定是有序的,然后从原先序列的第1个元素开始到第n-1个元素遍历,每次将当前元素插入到它之前序列中的合适位置。
void insert_sort(int a[], int n) {
for (int i = 1; i < n; ++i) {
if (a[i] < a[i - 1]) {
int j = i - 1, x = a[i];
a[i] = a[i - 1];
for (; x < a[j]; --j)
a[j + 1] = a[j];
a[j + 1] = x;
}
}
}
希尔-插入排序
希尔排序可以被认为是简单插入排序的一种改进。插入排序一个比较耗时的地方在于需要将元素反复后移,因为它是以1为增量进行比较的元素的后移可能会进行多次。一个长度为n的序列,以1为增量就是一个序列,以2为增量就形成两个序列,以i为增量就形成i个序列。希尔排序的思想是,先以一个较大的增量,将序列分成几个子序列,将这几个子序列分别排序后,合并,在缩小增量进行同样的操作,知道增量为1时,序列已经基本有序,这是进行简单插入排序的效率就会较高。希尔排序的维基词条上有一个比较好的解释例子如下:
// 原始序列
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
// 以5为增量划分,5列,每列即为一个子序列
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
// 对每一个子序列进行插入排序得到以下结果
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
// 恢复一行显示为
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
// 再以3为增量划分,3列,每列即为一个子序列
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
// 对每一个子序列进行插入排序得到如下结果
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
// 恢复一行为
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
// 然后再以1为增量进行插入排序,即简单插入排序
// 此时序列已经基本有序,分布均匀,需要反复后移的情况较少,效率较高
void shell_insert(int a[], int n, int dk) {
for (int i = dk, i < n; ++i) {
if (a[i] < a[i - dk]) {
int j = i - dk, x = a[i];
a[i] = a[i - dk];
for (; x < a[j]; j -= dk)
a[j + dk] = a[j];
a[j + dk] = x;
}
}
}
void shell_sort(int a[], int n) {
inr dk = n >> 1;
while (dk >= 1) {
shell_insert(a, n, dk);
dk = dk >> 1;
}
}
冒泡排序
冒泡排序的思想是,从第0个元素到第n-1个元素遍历,若前面一个元素大于后面一个元素,则交换两个元素,这样可将整个序列中最大的元素冒泡到最后,然后再从第0个到第n-2遍历,如此往复,直到只剩一个元素。
实现代码:
void bubble_sort(int a[], int n) {
bool flag = 1;
for (int i = 0; flag; ++i) {
flag = 0;
for (int j = n - 1; j > i; --j) {
if (a[j] < a[j - 1]) {
swap(a[j], a[j - 1]);
flag = 1;
}
}
}
}
选择排序
选择排序算法每次在未排序的数字中选择最大的那个数字放在数组末尾。
void select_sort(int n) {
for (int i = n - 1; i >= 0; i--) {
int idx = 0;
for (int j = 0; j <= i; ++j) {
if (A[j] > A[idx])
idx = j;
}
swap(A[i], A[j]);
}
}
快速排序
快速排序可能是最常被提到的排序算法了,快排的思想是,选取第一个数为基准,通过一次遍历将小于它的元素放到它的左侧,将大于它的元素放到它的右侧,然后对它的左右两个子序列分别递归地执行同样的操作。
快速排序利用分而治之的思想,它的最好和平均实际复杂度为O(nlogn),但是,如果选取基准的规则正好与实际数值分布相反,例如我们选取第一个数为基准,而原始序列是倒序的,那么每一轮循环,快排都只能把基准放到最右侧,故快排的最差时间复杂度为O(n2)。快排算法本身没有用到额外的空间,可以说需要的空间为O(1);对于递归实现,也可以说需要的空间是O(n),因为在递归调用时有栈的开销,当然最坏情况是O(n),平均情况是O(logn)。快速排序是不稳定的。
// 数组版模版
//调用方法
qsort(a, 0, n - 1);
void qsort(int a[], int l, int r) {
if (l >= r) return;
int i = l - 1, j = r + 1, x = a[l + rand() % (r - l + 1)];
while (i < j) {
while (a[++i] < x);
while (a[--j] > x);
if (i < j) swap(a[i], a[j]);
}
qsort(a, l, j);
qsort(a, j + 1, r);
}
归并排序
归并排序的思想是,利用二分的特性,将序列分成两个子序列进行排序,将排序后的两个子序列归并(合并),当序列的长度为2时,它的两个子序列长度为1,即视为有序,可直接合并,即达到归并排序的最小子状态。基于递归的实现如下:
//调用方法: merge_sort(nums, 0, nums.size()); 左闭右开
long long cnt = 0;
void merge_sort(vector<int>&a, int l, int r) {
if (l + 1 >= r) return;
int mid = l + (r - l) / 2;
merge_sort(a, l, mid);
merge_sort(a, mid, r);
vector<int> L(a.begin() + l, a.begin() + mid), R(a.begin() + mid, a.begin() + r);
for (int k = l, i = 0, j = 0; k < r; ++k) {
if (i == L.size()) a[k] = R[j++];
else if (j == R.size() || L[i] <= R[j]) a[k] = L[i++];
else {
a[k] = R[j++];
cnt += L.size() - i; // 用来统计逆序对数目
}
}
}
堆排序
堆排序利用的是二叉树的思想,所谓堆就是一个完全二叉树,完全二叉树的意思就是,除了叶子节点,其它所有节点都有两个子节点,这样子的话,完全二叉树就可以用一个一块连续的内存空间(数组)来存储,而不需要指针操作了。堆排序分两个流程,首先是构建大顶堆,然后是从大顶堆中获取按逆序提取元素。
- 数组元素从0开始,此时其左右儿子节点下标分别为
2 * i + 1和2 * i + 2。
void down(vector<int> &a, int n, int u) {
int t = u, l = u * 2 + 1, r = u * 2 + 2;
if (l < n && a[l] > a[t]) t = l;
if (r < n && a[r] > a[t]) t = r;
if (t != u) {
swap(a[u], a[t]);
down(a, n, t);
}
} //index from 0, left : 2*x + 1, right 2*x + 2
void heap_sort(vector<int> &a) {
for (int i = a.size() / 2 - 1; i >= 0; --i) {
down(a, a.size(), i);
}
for (int i = a.size() - 1; i > 0; --i) {
swap(a[0], a[i]);
down(a, i, 0);
}
}
- 数组元素从1开始,此时其左右儿子节点下标分别为
2 * i和2 * i + 1。
void down(vector<int>& nums, int n, int u) {
int t = u, l = u * 2, r = u * 2 + 1;
if (l < n && nums[l] > nums[t]) t = l;
if (r < n && nums[r] > nums[t]) t = r;
if (t != u) {
swap(nums[u], nums[t]);
down(nums, n, t);
}
}
void up(vector<int>& nums, int n, int u) {
while (u > 1 && h[u] > h[u/2]) {
swap(nums[u], nums[u/2]);
u /= 2;
}
}
实现堆的操作
下表从1开始
const int N = 1e5 + 10;
struct Heap{
using T = int;
T h[N], n;
Heap(): n(0) {}
Heap(vector<T>& v) {
build(v);
}
void down(int n, int u) {
int t = u, l = u * 2, r = u * 2 + 1;
if (l <= n && h[l] > h[t]) t = l;
if (r <= n && h[r] > h[t]) t = r;
if (t != u) {
swap(h[u], h[t]);
down(n, t);
}
}
void up(int u) {
if (u > n) return;
while (u > 1 && h[u] > h[u/2]) {
swap(h[u], h[u/2]);
u /= 2;
}
}
void insert(T x) {
h[++n] = x;
up(n);
}
void delect(int u) {
int t = h[u];
h[u] = h[n--];
if (h[u] > t) up(u);
else down(n, u);
}
void build(vector<T>& v){
n = v.size();
for (int i = 1; i <= n; ++i) {
h[i] = v[i - 1];
}
for (int i = n / 2; i >= 1; --i) {
down(n, i);
}
}
vector<T> sort() {
for (int i = n; i > 1; --i) {
swap(h[1], h[i]);
down(i - 1, 1);
}
return vector<T>(h + 1, h + n + 1);
}
};
建堆时间复杂度
- 自顶向下建堆时,最下层n/2个元素最多都可能要上升log2(n)层,所以时间复杂度为O(nlog(n)).
- 自底向上建堆时
- 最下层n/2个元素不需要动
- 次下层n/4个元素最多下沉1层
- 倒数第三层的n/8个元素最多下沉2层
以此类推,所有元素总的移动次数最多为 S = 0*(n/2) + 1*(n/4) + 2*(n/8) + ...
这是一个常见的、等差数列与等比数列相乘后的求和问题,采样错位相减法:
2S = 0*n + 1*(n/2) + 2*(n/4) + ...
2S - S = 1*(n/2) + 2*(n/4) + 1*(n/8) + ...
S = n
彩虹排序
给定一个有n个对象(包括k种不同的颜色,并按照1到k进行编号)的数组,将对象进行分类使相同颜色的对象相邻,并按照1,2,…k的顺序进行排序。
- 不能使用代码库中的排序函数来解决这个问题
- k <= n
1.可以借助一个O(k)的数组bucket,然后扫一遍原来的数组,统计每一种颜色有多少个存放在数组bucket里面,然后题目要求把颜色排序,其实就是再把b里面的统计重新输出到原来的数组就好了。
- 时间复杂度:O(n+k) = O(n).
void sortColor2(vector<int>& colors, int k) {
vector<int> cnt(k + 1);
for (int x : colors) cnt[k]++;
for (int i = 1, j = 0; i <= k; j += cnt[i++])
fill(colors.begin() + j, colors.begin() + j + cnt[i], i);
}
- 如果不能使用额外数组,可以用快速排序+归并排序思想,quickSort的思想在于partition进行分割,mergeSort的思想在于直接取中间(这里表现为取中间大小的数),分为左右两个相等长度的部分。区别在于partition的判定条件变为了 中间大小的元素而不是中间位置的元素,因此等号的取值可以只去一边也不会有影响。
- qsort实现的是将colors数组的索引范围
l到r位置排序,排序的大小范围是b到e.- 时间复杂度为
O(n*log(k))
void qsort(vector<int>& v, int l, int r, int b, int e) {
if (l == r || b == e) return;
int mid = b + (e - b) / 2, i = l, j = r;
while (i <= j) {
while (i <= j && v[i] <= mid) i++;
while (i <= j && v[j] > mid) j--;
if (i <= j) {
swap(v[i], v[j]);
i++,j--;
}
}
qsort(v, l, j, b, mid);
qsort(v, i, r, mid + 1, e);
}
void sortColors2(vector<int> &colors, int k) {
if (colors.size() <= 1) return;
qsort (colors, 0, colors.size() - 1, 1, k);
}
第k大数
第k小数
给定一个长度为 n的整数数列,以及一个整数 k,请用快速选择算法求出数列从小到大排序后的第k个数。
- 1 <= k <= n <= 1e5
int kth_ele(vector<int> &a, int l, int r, int k) {
if (l == r) return a[l];
int i = l - 1, j = r + 1, x = a[l + rand() % (r - l + 1)];
while (i < j) {
while (a[++i] < x);
while (a[--j] > x);
if (i < j) swap(a[i], a[j]);
}
int s = j - l + 1;
return k <= s ? kth_ele(a, l, j, k) : kth_ele(a, j + 1, r, k - s);
}
// cout << kth_ele(a, 0, n - 1, k);
第k大数
给定一个整数数组a,同时给定它的大小n和要找的K(K在1到n之间),请返回第K大的数,保证答案存在
int kth_ele(vector<int> &a, int l, int r, int k) {
if (l == r) return a[l];
int i = l - 1, j = r + 1, x = a[l + rand() % (r - l + 1)];
while (i < j) {
while (a[++i] < x);
while (a[--j] > x);
if (i < j) swap(a[i], a[j]);
}
int s = j - l + 1;
return k <= s ? kth_ele(a, l, j, k) : kth_ele(a, j + 1, r, k - s);
}
int findKth(vector<int>& a, int n, int K) {
return kth_ele(a, 0, a.size() - 1, a.size() - K + 1);
}
最小k个数
按任意顺序返回最小的k个数, 0 <= k <= len(arr)
不要求有序的话,期望时间复杂度为O(n)
int kth_ele(vector<int> &a, int l, int r, int k) {
if (l >= r) return a[l];
int i = l - 1, j = r + 1, x = a[l + rand() % (r - l + 1)];
while (i < j) {
while (a[++i] < x);
while (a[--j] > x);
if (i < j) swap(a[i], a[j]);
}
int s = j - l + 1;
return k <= s ? kth_ele(a, l, j, k) : kth_ele(a, j + 1, r, k - s);
}
vector<int> smallestK(vector<int>& a, int k) {
if (k == 0) return {};
kth_ele(a, 0, a.size() - 1, k);
return vector<int>(a.begin(), a.begin() + k);
}
使用 nth_element
vector<int> smallestK(vector<int>& a, int k) {
nth_element(a.begin(), a.begin() + k, a.end());
return vector<int>(a.begin(), a.begin() + k);
}
数据流中的中位数
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。 例如,
[2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
class MedianFinder {
priority_queue<int> maxq;
priority_queue<int, vector<int>, greater<int>> minq;
public:
MedianFinder() {}
void addNum(int num) {
maxq.push(num);
minq.push(maxq.top());
maxq.pop();
if (maxq.size() < minq.size()) {
maxq.push(minq.top());
minq.pop();
}
}
double findMedian() {
return maxq.size() > minq.size() ? (double)maxq.top() : (maxq.top() + minq.top()) * 0.5;
}
};
总结