二维数组遍历系列

2020-08-17 | 阅读：次

===

Index

螺旋矩阵
螺旋矩阵II
螺旋矩阵III
旋转图像
二维数组右上左下遍历
对角线遍历
神奇的幻方
蛇形填充数组

螺旋矩阵

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

    vector<int> spiralOrder(vector<vector<int>>& mx) {
        int m = mx.size(), n = m ? mx[0].size() : 0;
        int u = 0, d = m - 1, l = 0, r = n - 1, p = 0;
        vector<int> res(m * n);
        while (u <= d && l <= r) {
            for (int i = l; i <= r; ++i) res[p++] = mx[u][i];
            if (++u > d) break;
            for (int i = u; i <= d; ++i) res[p++] = mx[i][r];
            if (--r < l) break;
            for (int i = r; i >= l; --i) res[p++] = mx[d][i];
            if (--d < u) break;
            for (int i = d; i >= u; --i) res[p++] = mx[i][l];
            ++l;
        }
        return res;
    }

螺旋矩阵2

leetcode 59

给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ans(n, vector<int>(n, 0));
        int t = 1, i = 0, j = 0, m = n * n;
        while (t <= m) {
            while (j < n && !ans[i][j]) ans[i][j++] = t++;
            j--; i++;
            while (i < n && !ans[i][j]) ans[i++][j] = t++;
            i--; j--;
            while (j >= 0 && !ans[i][j]) ans[i][j--] = t++;
            j++; i--;
            while (i >= 0 && !ans[i][j]) ans[i--][j] = t++;
            i++; j++;
        }
        return ans;
    }

螺旋矩阵3

leetcode 885

在 R 行 C 列的矩阵上，我们从 (r0, c0) 面朝东面开始

这里，网格的西北角位于第一行第一列，网格的东南角位于最后一行最后一列。

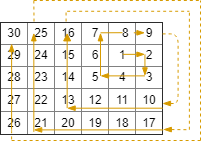
现在，我们以顺时针按螺旋状行走，访问此网格中的每个位置。

每当我们移动到网格的边界之外时，我们会继续在网格之外行走（但稍后可能会返回到网格边界）。

最终，我们到过网格的所有 R * C 个空间。

按照访问顺序返回表示网格位置的坐标列表。

    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        vector<vector<int>> ans { {r0, c0} };
        int dx = 0, dy = 1, n = 0, step = 1;
        while (ans.size() < R * C) {
            for (int i = 0; i < step; ++i) {
                r0 += dx;
                c0 += dy;
                if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) 
                    ans.push_back({r0, c0});
            }
            ++n;
            if (n % 2 == 0) 
                ++step;
            swap(dx, dy);
            dy = -dy;
        }
        return ans;
    }

旋转图像

leetcode 48

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

方法一：

    void rotate(vector<vector<int>>& mat) {
        int n = mat.size();
        for (int i = 0; i < (n >> 1); i++) {
            for (int j = i; j < n-1-i; j++) {
                int tmp = mat[i][j];
                mat[i][j] = mat[n - 1 - j][i];
                mat[n - 1 - j][i] = mat[n - 1 - i][n - 1 - j];
                mat[n - 1 - i][n - 1 - j] = mat[j][n - 1 - i];
                mat[j][n - 1 - i] = tmp;
            }
        }
    }

方法二：先转置，再逆序

    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for(int i = 0; i < n; i++){
            for(int j = 0; j < i; j++){
                swap(matrix[i][j], matrix[j][i]);
            }
        }
        for(int i = 0; i < n; i++){
            reverse(matrix[i].begin(), matrix[i].end());
        }
    }

方法三：先水平反转，再主对角线反转

    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }

二维数组右上左下遍历

noi 21

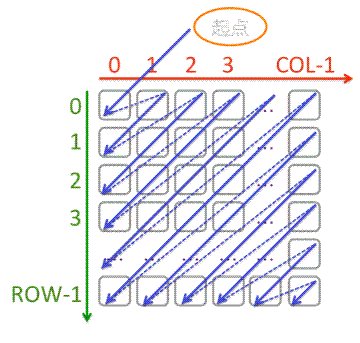
给定一个row行col列的整数数组array，要求从array[0][0]元素开始，按从左上到右下的对角线顺序遍历整个数组。

    vector<int> traverse(vector<vector<int>>& mat) {
        int n = mat.size(), m = mat[0].size();
        vector<int> res;
        for (int i = 0; i < n + m - 2; ++i) {
            for (int j = i; j >= 0; --j) {
                if (j < m && i - j < n) 
                    res.push_back(mat[i - j][j]);
            }
        }
        return res;
    }

对角线遍历

leetcode 498

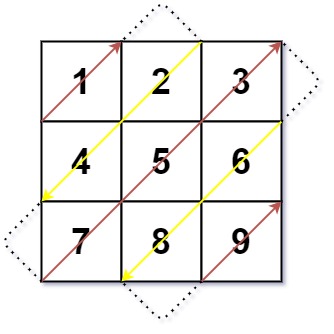
给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        int n = mat.size(), m = mat[0].size();
        vector<int> res;
        for (int i = 0; i <= n + m - 2; ++i) {
           if (i % 2 == 0) {
               for (int j = 0; j <= i; ++j) {
                   if (j < m && i - j < n) res.push_back(mat[i-j][j]);
               }
           } else {
               for (int j = i; j >= 0; --j) {
                   if (j < m && i - j < n) res.push_back(mat[i-j][j]);
               }
           }
        }
        return res;
    }
};

神奇的幻方

noi 22

幻方是一个很神奇的N*N矩阵，它的每行、每列与对角线，加起来的数字和都是相同的。我们可以通过以下方法构建一个幻方。（阶数为奇数） 1.第一个数字写在第一行的中间 2.下一个数字，都写在上一个数字的右上方：

如果该数字在第一行，则下一个数字写在最后一行，列数为该数字的右一列

如果该数字在最后一列，则下一个数字写在第一列，行数为该数字的上一行

如果该数字在右上角，或者该数字的右上方已有数字，则下一个数字写在该数字的下方

    vector<vector<int>> megic(int n) {
        int m = 2 * n - 1, N = m * m, ipre, jpre;
        vector<vector<int>> a(m, vector<int>(m));
        for (int i = 0; i < N; ++i) {
            if (i == 0) {
                ipre = 0; jpre = n - 1;
            } else if (ipre == 0 && jpre != m - 1) {
                ipre = m - 1; jpre = jpre + 1;
            } else if (jpre == m - 1 && ipre) {
                ipre = ipre - 1; jpre = 0;
            } else if ((ipre == 0 && jpre == m - 1) || a[ipre - 1][jpre + 1]) {
                ipre = ipre + 1; jpre = jpre;
            } else {
                ipre = ipre - 1; jpre = jpre + 1;
            }
            a[ipre][jpre] = i + 1;
        }
        return a;
    }

蛇形填充数组

noi 24

用数字1,2,3,4,…,nn这n2个数蛇形填充规模为nn的方阵。

蛇形填充方法为：

对于每一条左下-右上的斜线，从左上到右下依次编号1,2,…,2n-1；按编号从小到大的顺序，将数字从小到大填入各条斜线，其中编号为奇数的从左下向右上填写，编号为偶数的从右上到左下填写。

比如n=4时，方阵填充为如下形式：

vector<vector<int>> fill_array(int n) {
    vector<vector<int>> a(n, vector<int>(n));
    int t = 1;
    for (int i = 0; i < 2 * n - 2; ++i) {
        for (int j = i; j >= 0; --j) {
            if (j < n && i - j < n) {
                if (i & 1) a[i - j][j] = t++;
                else a[j][i - j] = t++;
            }
        }
    }
    return a;
}

king-yyf